Método algebraico de suma y resta – Matemáticas 1
Este método se aplica en la resolución de sistemas de dos ecuaciones con dos incógnitas o incluso con tres
Observemos el siguiente sistema:
Al intentar hacer la gráfica se observa un problema de escala y por lo tanto es complicado definir las dos ecuaciones en el plano cartesiano, al realizar esto causaría que probablemente resulte una solución errónea, para esto se debe de emplear técnicas algebraicas que permitan conocer la solución al sistema.
Podemos observar que el sistema posees el mismo coeficiente en la variable “y”, con esto podemos sumar o restar cada uno de los miembros para obtener una tercera ecuación más sencilla.
Al simplificar el resultado se obtiene la igualdad de la ecuación y así poder averiguar el valor de x:
Cuando se encuentra el valor de x, se sustituye “x=1” en cualquiera de las dos ecuaciones:
De esta manera obtenemos el par ordenado (1, 1), el cual es la solución al sistema de ecuaciones.
En este caso se sumaron las dos ecuaciones para eliminar una de las variables, porque los signos de sus coeficientes (3 y -3) eran contrarios, si estos signos hubieran sido iguales, se habrían restado.
Ejemplo:
Tenemos el siguiente sistema de ecuaciones y es necesario hallar las ecuaciones equivalentes.
Solución:
Para solucionar este problema, vamos a emplear una estrategia la cuan consiste en multiplicar la primera ecuación por 3 y la segunda por 2, con esto lograremos que la variable “y” tenga el mismo coeficiente y poder eliminarla
Las ecuaciones equivalentes que forman el sistema son:
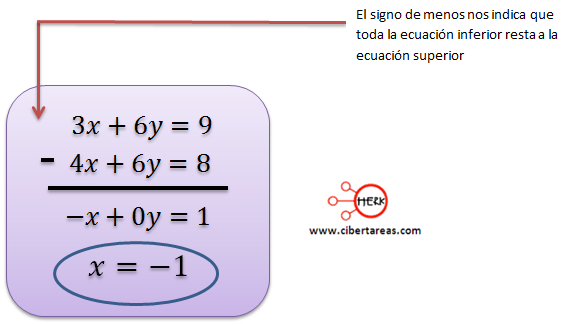
Al restar estas ecuaciones obtendremos el valor de “x”
Al momento de obtener el valor de “x”, se sustituye en cualesquiera de las dos ecuaciones para poder definir el calor de “y”
Con esto tenemos el par ordenado (-1, 2) el cual es la solución para el sistema de ecuaciones.

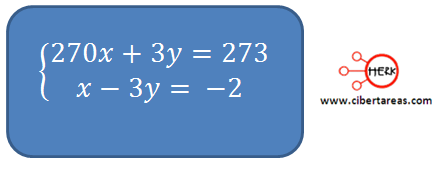
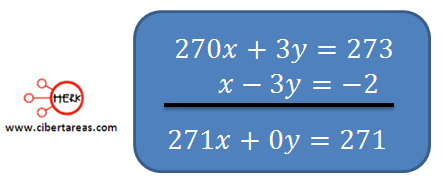
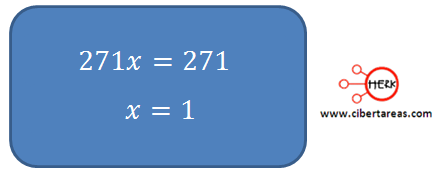
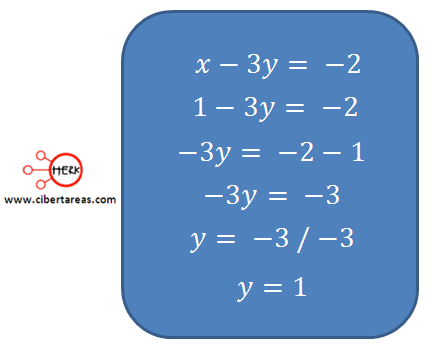

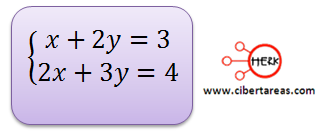
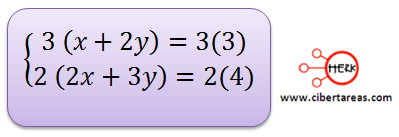
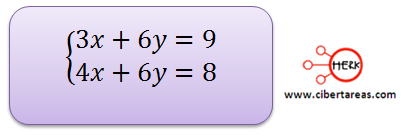


kim sandoca gisma says:
muy buena la pagina me sirvio un buen para mi tarea de investigacion y la neta si aprendí