Rectas tangentes a un circulo en Matemáticas 2

La circunferencia tiene asociadas varias:

-Rectas

-Segmentos de recta

-Ángulos importantes

Es muy común escuchar la expresión: se salió por la tangente, esto se refiera cuando una persona que emite un comentario sin ninguna relación con el tema de conversación

Un ejemplo de la presencia del concepto de tangente se puede observar cuando un niño juega con una llanta o rin de bicicleta:

Es importante aclarar que si una circunferencia tiene infinidad de puntos, se piensa que tendría una infinidad de rectas tangentes, pero no se trata de esta situación, sino de considerar las rectas tangentes a un círculo, a partir de la posición del punto por donde pasan estas rectas tangentes, bajo estas circunstancias tenemos:

Caso 1

-Construcción de la recta tangente a una circunferencia dado un punto P determinado de ella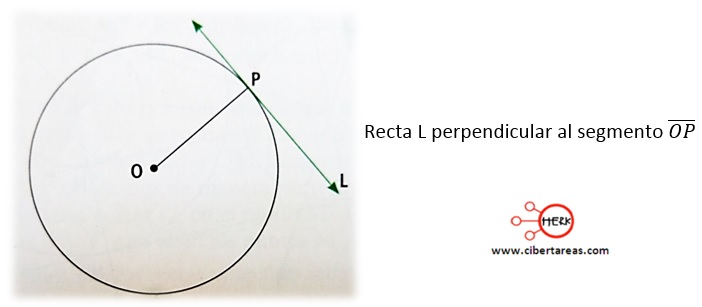

1.- Se traza y prolonga el radio  de la circunferencia

2.- Se traza la recta perpendicular L al segmento  que pasa por el punto P

Conclusión

-La perpendicular trazada es la recta L tangente a la circunferencia, cuyo punto de tangencia es P

Caso 2

-Construcción de la recta tangente a la circunferencia, dado un punto P en el exterior de ella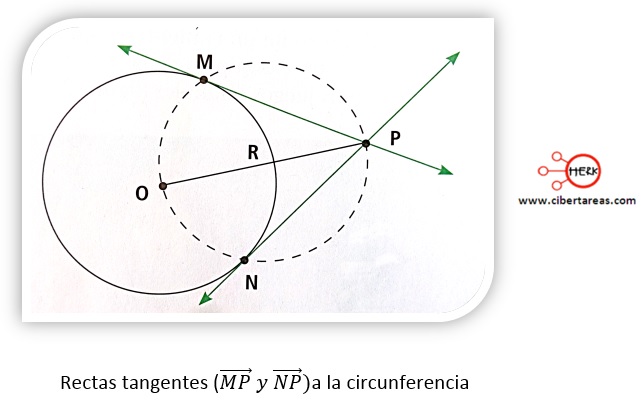

1.- Se traza el segmento

2.- se determina el punto medio R del segmento

3.- Con centro en R se traza la circunferencia de radio RP que corta a la inicial en dos puntos de tangencia: M y N

4.- Se traza las rectas 

Conclusión

-Las rectas   son tangentes a la circunferencia dada

Caso 3

-Construcción de las tangentes comunes (T, T´), exteriores a dos circunferencias C₁ y C₂

1.- Se traza una circunferencia C₃ de radio igual a la diferencia entre los radios de las circunferencias dadas: (R₂ – R₁), concéntrica (mismo centro) a la circunferencia mayor C₂

2.- Se utiliza el procedimiento del caso anterior para trazar las tangentes a C₃, y con origen en O, así se obtienen los puntos de tangencia M y N

3.- Se traza el segmento de recta  y se prolonga hasta cortar la circunferencia C₂, determinando el punto M´

4.- Se traza la linea  y se prolonga hasta cortar la circunferencia C₂, determinando el punto N´

5.- Se traza por O una paralela (L₁) a  que corte C₁, y se determina ahora el punto N´´

6.- Se trazan las rectas T y T´que unen los puntos M´´, M´y N´´, N´

Conclusión

-Así se obtienen las dos rectas tangentes exteriores a las circunferencias

Caso 4

-Construcción de las tangentes comunes e interiores a dos circunferencias dadas C₁ y C₂

1.- Se traza una circunferencia C₃ de radio igual a la suma de los radios de las circunferencias dadas: R₂ + R₁, con centro en O

2.- Se determinan las tangentes a C₃, con origen en O´, y se obtienen los puntos de tangencia M y N

3.-Se traza la línea de radio  que corta a la circunferencia C₁ en el punto M´

4.- Se traza la línea de radio  que corta a la circunferencia C₁ en el punto N´

5.- Se traza por O´una paralela (L₁) a   hasta cortar C₂ en el punto M´´

6.- Se trazan las rectas T y T´que unen los puntos M´, N´´ y M´´, N´

Conclusión

-Así se obtienen las dos rectas tangentes interiores a las circunferencias dadas