Les comparto esta informacion

Agradecemos tus comentarios y sugerencias para mejorar nuestra pagina 🙂

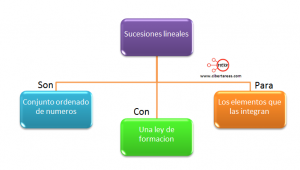
Series y sucesión lineal

Tenemos como ejemplos:

1.- Serie de números:

2, 4, 6, 8….

Donde el número 2 es el primer término.

La ley de formación la obtenemos al sumar un valor de 2 a cada paso.

2.- Serie de números:

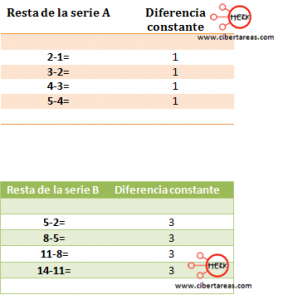
A) 1, 2, 3, 4, 5

B) 2, 5, 8, 11, 14

Si restamos el sucesor con el antecesor obtenemos:

La primera serie de números inicia con 1 y la segunda con 2

Si se elabora un formula en la que incluya la diferencia que se produce en la segunda sucesión y su primer término, entonces se puede hallar los elementos de esa serie, incluyendo el ultimo o el n-esimo termino.

1.- Tenemos que el n-esimo término se obtiene a partir del primero y de las diferencias comunes que es una constante.

2.- Este término permite encontrar cualquier valor al sustituir n por otro dato numérico.

3.- La sucesión aritmética presenta una constante d, que es la diferencia común entre los factores que componen la serie.