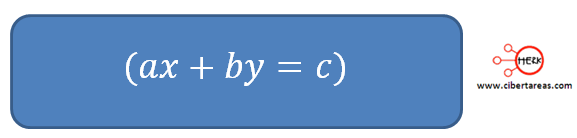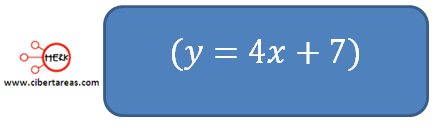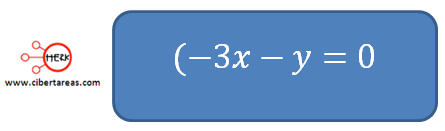Sistemas de ecuaciones simultáneas lineales con dos incógnitas – Matemáticas 1
Las ecuaciones lineales con dos incógnitas con aquellas que adoptan la forma:
Dónde:
La representación gráfica de estas ecuaciones son rectas perfectamente identificables con el plano cartesiano, y la intersección de dos o más rectas adquiere un significado especial en el mundo algebraico.
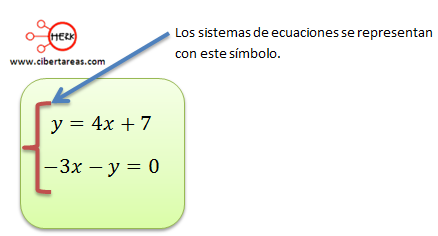
Al tener un conjunto de ecuaciones lineales y se requiere hallar soluciones comunes, se habla de un sistema de ecuaciones simultaneas lineales.
En general, en estas ecuaciones se encuentran dos o más incógnitas, y cada una puede tener infinitas soluciones.
Al encontrar la solución a un sistema, o llegar a la conclusión de que no existe tal solución, se logra luego de haber resuelto un sistema de ecuaciones.
Las ecuaciones lineales con dos incógnitas, tienen diversas soluciones para expresar un equilibrio y cumplir las propiedades de la igualdad.
Vamos a analizar la ecuación:
Esta ecuación admite o tiene varias soluciones:
Tenemos otra ecuación:
Esta ecuación también admite o tiene varias soluciones:
Al considerar las dos ecuaciones como un sistema de ecuaciones, las condiciones varían y también las soluciones:
Tenemos que la solución del sistema se alcanza al momento de encontrar una solución común.
Para este ejemplo la única solución válida es:
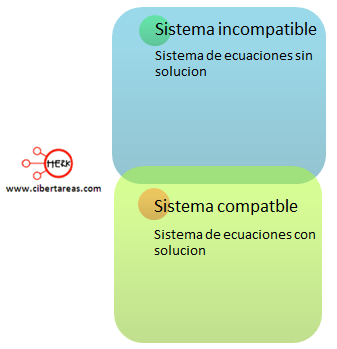
Tenemos como consecuencia que el sistema es compatible.
Un sistema de ecuaciones lineales compatible es determinado si tiene una solución única y es indeterminado si posee infinitas soluciones.