Suma de medidas de ángulos en Matemáticas 2

Como se sabe, el movimiento de rotación de la Tierra genera el día y la noche, si se observa una imagen de la tierra desde algún satélite, se podrá observar que mientras hay luz solar en parte de África y Europa, en regiones de los mismos continentes se encienden las luces artificiales, esto ocurre cada 24 horas, también se puede afirmar que en un giro de 360° de la tierra se muestra el movimiento de la luz y las sombras, como se muestra en la siguiente imagen:

Como sabemos, un día se compone de 24 horas y un giro completo son 360°, se puede establecer una razón para definir un valor que permitirá reconocer cuantos grados gira la tierra por hora: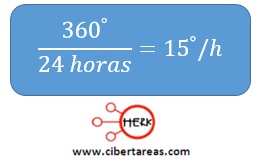

Con estos datos podemos analizar la siguiente tabla comparativa:

Al observar los datos, y si se suman por columna, se encuentra la importancia de esto datos:

La importancia en esta suma de los ángulos, es que equivale a 60°, es decir, a 4 horas del giro de la tierra

Otro ejemplo es:

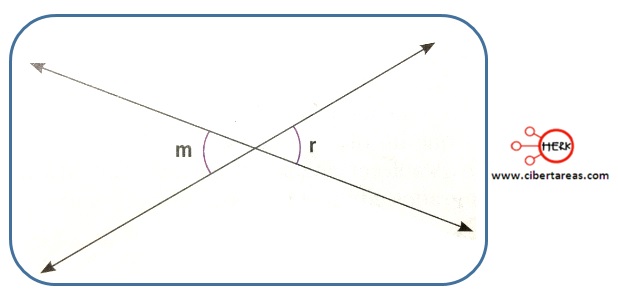
-Es necesario demostrar que si

Solución:

-Datos

son ángulos

-Ambos son opuestos por el vértice

-Entonces 

-Análisis

-Lo que se necesita demostrar es:

-Para demostrarlo se deben incluir un nuevo ángulo en la gráfica, sea este 

-Al analizar tenemos la siguiente gráfica inicial

-De acuerdo con el concepto de ángulo llano, se puede definir que:

-En estas condiciones se establece una igualdad del siguiente orden:

-Al despejar , se obtiene:

-Síntesis interpretativa

-La igualdad anterior permite eliminar la variable  y por tanto se demuestra que:

-Esto quiere decir que si dos ángulos son opuestos por el vértice entonces serán iguales

Podemos manejar otro ejemplo:

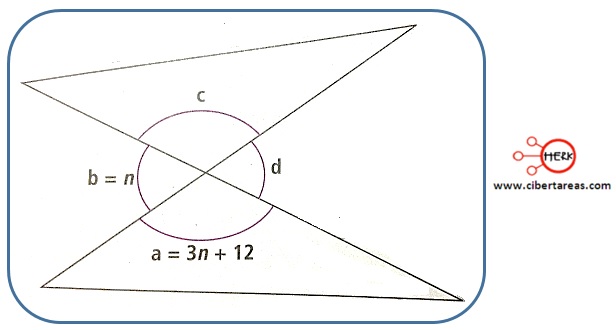
-Se necesita encontrar el valor de cada ángulo de los siguientes triángulos si se observa que son opuestos por el vértice los pares

Solución

-Datos

b y d

-Análisis

-Al analizar, observamos que:

-De estas cuatro igualdades se busca la que nos permita formular una ecuación para encontrar los valores correspondientes, la única que sirve es: , ya que tenemos los datos necesarios para hallar esos ángulos

-Se sabe que:

b = n

a = 3n + 12

-Al tomar en cuenta la igualdad: , se hace las sustituciones respectivas para despejar la variable n:

3n + 12 + n = 180

4n + 12 = 180

4n = 180 – 12

4n = 168

n = 168/4

n = 42

-Síntesis interpretativa

-Al encontrar los valores correspondientes de cada ángulo, tenemos que:

-Para :

-Para :

-Como los pares  son ángulos opuestos por el vértice, debe cumplirse que:

En la geometría, los aportes teóricos y prácticos anteriores permiten sintetizar la siguiente información relacionada con los ángulos y su clasificación, según la posición de sus lados y cuando se oponen los ángulos por un mismo vértice

Ángulos adyacentes

-Los ángulos son adyacentes cuando dos ángulos conservan un lado común y un mismo vértice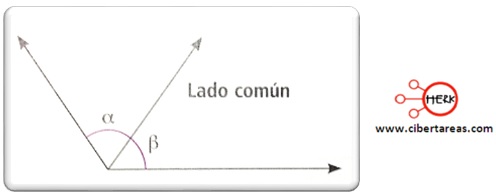

Ángulos opuestos por un vértice

-En este caso se cumple la congruencia entre dos ángulos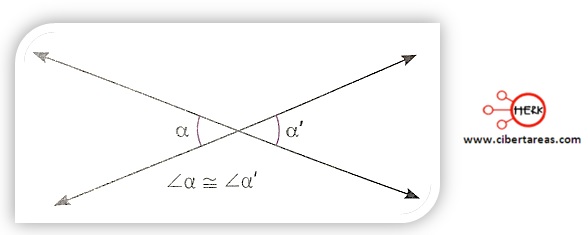

Clasificación de los ángulos por la suma de sus medidas

Ángulos complementarios

-Cuando la suma de los ángulos da como resultado 90°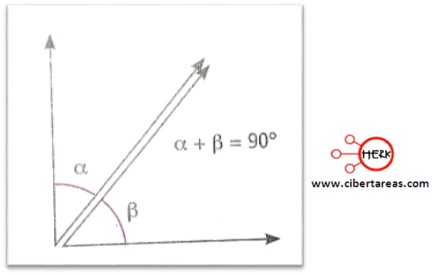

Ángulos suplementarios

-La suma de los ángulos da como resultado 180°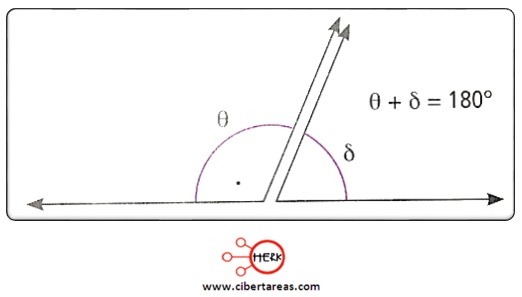

Es importante considera la sima de los ángulos para poder averiguar el valor de un ángulo como incógnita, para llegar a estas definiciones es fundamental realizar representaciones visuales y asimilar los conceptos matemáticos de manera lógica, asi no se tendrá que recurrir tana a la memoria