Medición de ángulos en el sistema sexagesimal en Matemáticas 2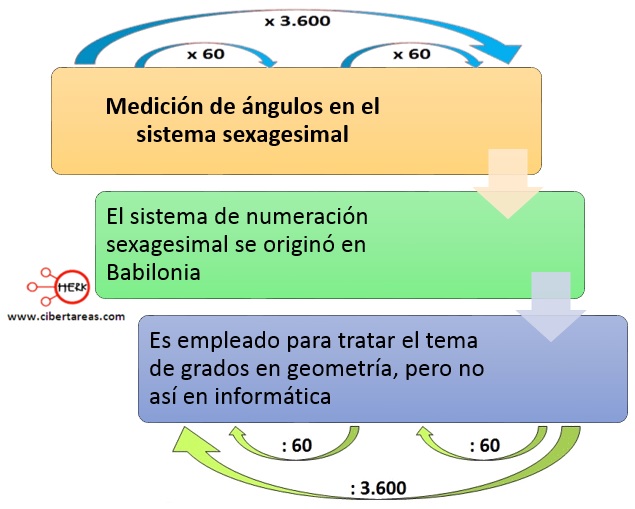

Los conceptos teóricos asimilados hasta el día de hoy, permiten distinguir que hay valores asociados con este sistema de numeración, por ejemplo:

-Al hablar del ángulo llano

-Se puede concebir como el producto de:

-(60° ∙ 3 = 180°)

-Cuando se refieren a circunferencias (360°) siempre se considera el sistema sexagesimal

-Su aplicación será trascendental para el tema de triángulos

Ejemplo 1

-El sistema sexagesimal se aplica en una situación cotidiana en la escuela

-El maestro dejo como investigación, el análisis de los botones de una calculadora científica

-Al analizar las teclas de la calculadora, Juan y Carlos se preguntaron para qué sirve la tecla:

-Al no saber interpretar lo que aparecía en la pantalla al presionar dicha tecla, fueron a consultar a sus compañeros de semestres arriba

Solución

-El compañero de semestres mas adelante, pidió Ju y Carlos que digitaran el número 30 en la calculadora y luego oprimieran la tecla:

-El resultado desplegado por la calculadora fue 30°0°0°

-El mecanismo de la calculadora emplea el sistema sexagesimal y así se determina el valor 30°0’0″ (treinta grados, cero minutos y cero segundos)

-Algebraicamente se puede expresar así:

-X° Y’ Z”

-Y sí Y’ equivale a 60, entonces el valor de X° aumenta uno, es decir: (X + 1)°

-Carlos razonó y comentó que si tenía la serie: 30°60’15”, entonces equivaldría a 31°0’15”

-Posteriormente el compañero de semestres adelante les propuso que teclearan el número 30.5 y la tecla en cuestión, el resultado fue: 30°30’0″

-Con esto surge una pregunta: ¿Cómo se interpretan este resultado?

-La mitad de una unidad (0.5) estaba asociada con la mitad de un grado (30´), pues la parte entera se asocia con los grados, y la parte decimal con los minutos y segundos

-Tenemos entonces que al escribir 30.25, el resultado sería:

-30°15’0″.

-Si bien 0.25 es la cuarta parte de una unidad y 15′ es la cuarta parte de un grado, no se puede establecer siempre una relación de este tipo, porque entre cada entero positivo hay una infinidad de números

 -Para que quede más claro lo anterior, es necesario analizar el siguiente esquema, aunque incompleto puede explicar paso a paso ciertas conversiones: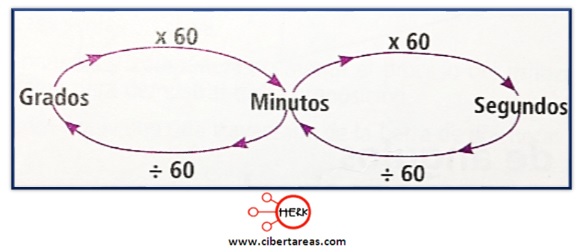

-Al analizar el esquema anterior, podemos observar que si se tiene una cantidad en grados y al pasarlos a minutos, se debe multiplicar el número por 60, pero si era el proceso inverso tenía que dividirlos, esto mismo ocurre para pasar de minutos a segundos

-Al pasar de grados a segundos debe obtenerse el producto de los dos valores del medio, en otras palabras (60 ∙ 60 = 3600), esto quiere decir que para pasar de grados a segundos se debe multiplicar por 3 600 y el proceso inverso será dividir entre esta misma cantidad