Suma de vectores por el método de las componentes en Física 1

En muchas situaciones físicas es necesario sumar dos o más magnitudes vectoriales concurrentes, en estos casos, para obtener la resultante se emplea el método de las componentes, el cual es un método general para sumar este tipo de magnitudes vectoriales

Pasos del método de las componentes

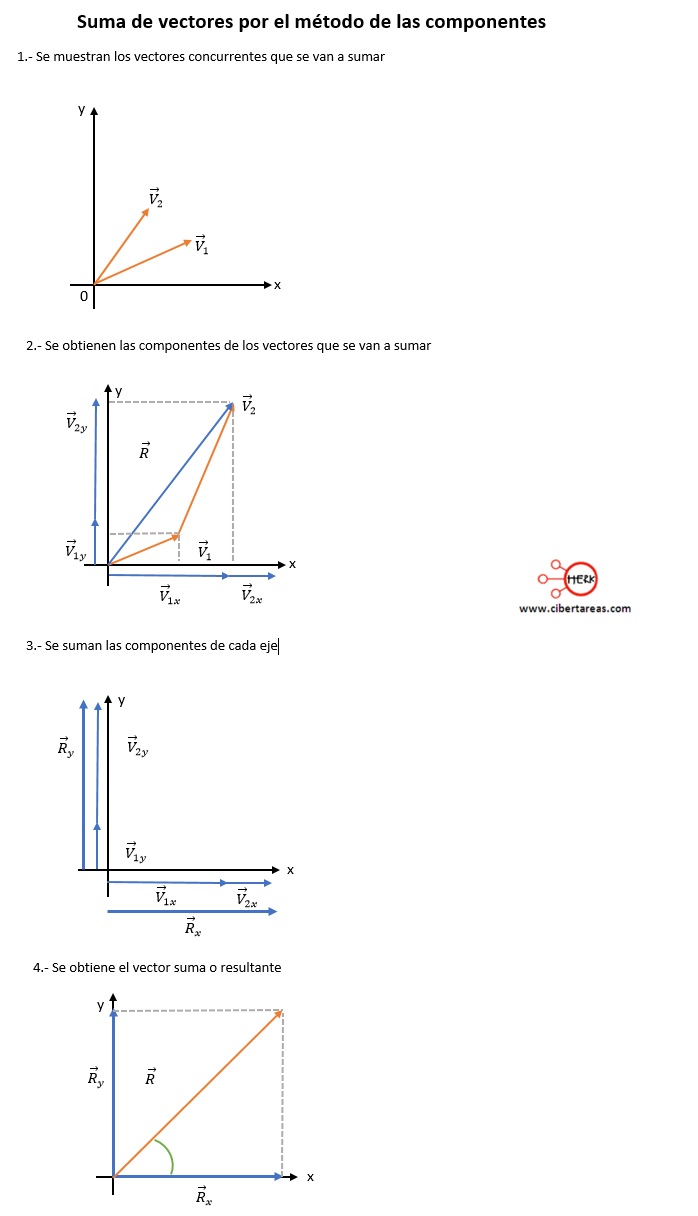
1.- Dibujar un esquema de los vectores que se van a sumar

2.- Seleccionar el sistema de coordenadas cartesianas que facilite los cálculos, de manera que su origen coincida con el origen de los vectores concurrentes

3. Hacer una tabla que concentre los datos, cálculos y resultados. Ejemplo: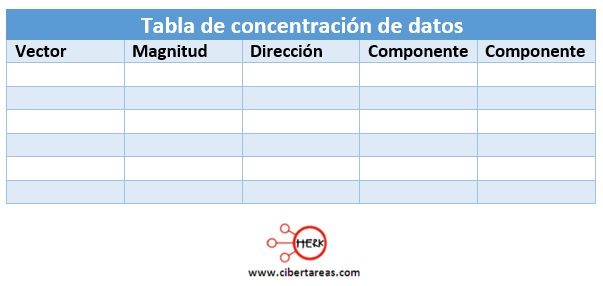

4.- Determinar el ángulo de cada vector con respecto al eje x, como se muestra en la siguiente imagen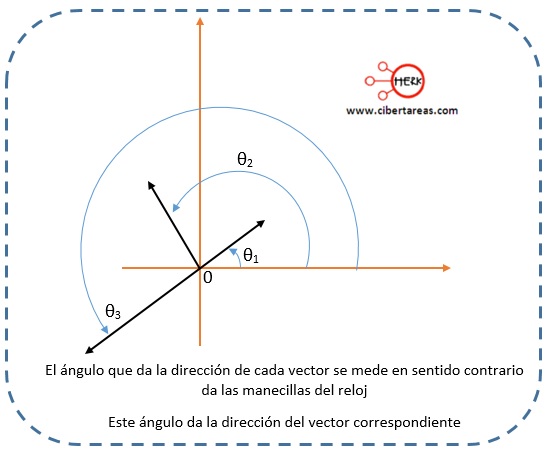

5.- Registrar la magnitud y dirección de cada vector en la tabla de valores

6.- Calcular las magnitudes de las componentes cartesianas de cada vector mediante las siguientes ecuaciones:

7.- Registrar los resultados obtenidos en la tabla de valores

8.- Sumar las magnitudes de las componentes de cada eje de coordenadas, tomando en cuenta el signo algebraico

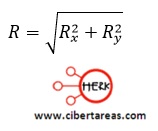
9.- Calcular la magnitud del vector resultante  mediante el teorema de Pitágoras

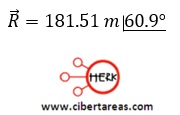
10.- Calcular la dirección del vector resultante (R) mediante la siguiente ecuación trigonométrica:

Este método de las componentes se muestra en la siguiente imagen:

Ejemplo:

-Problema

Determinar la resultante del sistema de vectores

Es necesario calcular la resultan de los cuatro vectores mostrados en la siguiente figura: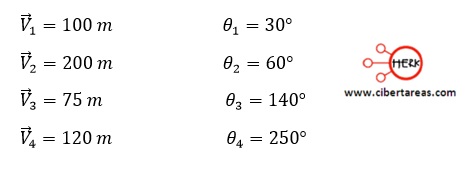

Solución

Para obtener la magnitud del vector resultante