Teorema del ángulo central y el ángulo semi-inscrito en Matemáticas 2

Existe una  incógnita, la cual nos cuestiona que se esté teorema solo es válido para ángulos  inscritos y centrales, o también lo es para un ángulo semi-inscrito y su correspondiente ángulo central, para esto es necesario observar la sucesión de imágenes siguiente: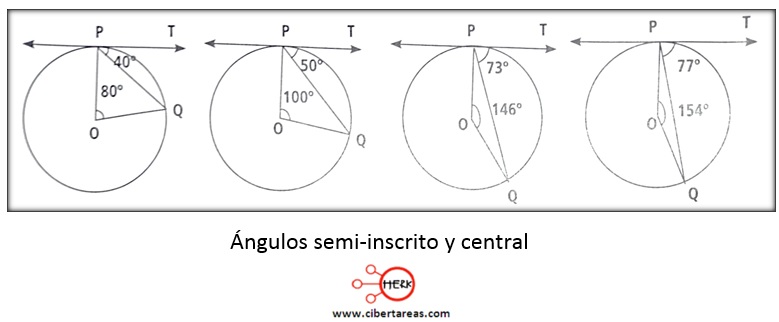

Se puede observar que el ángulo semi-inscrito siempre es menor que 90°, exactamente, este ángulo es la mitad del ángulo central que abraca el mismo arco de circunferencia

Esta demostración se dividirá en dos casos:

Caso 1

-El ángulo semi-inscrito es agudo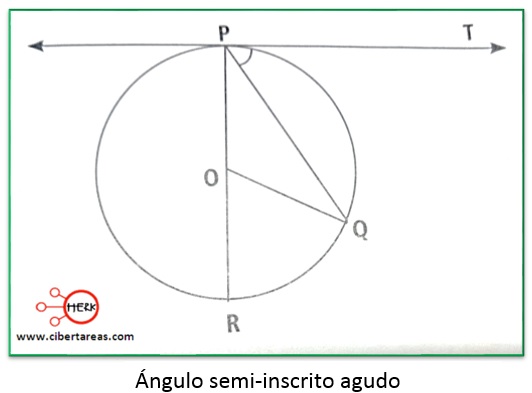

Hipótesis

T es una recta tangente a la circunferencia en el punto P, y   es una recta secante de esta circunferencia

Tenemos que:

Tesis

1.- Trazamos el diámetro  que corta a la circunferencia en el punto R

2.- , forman un ángulo llano

3.- , o sea, forman producto de la igualdad anterior

4.- , por el teorema

5.-  es un diámetro perpendicular a la recta T en el punto P

6.- , multiplicamos por 2 la igualdad anterior

7.- , producto de las igualdades anteriores

8.-

Caso 2

El ángulo semi-inscrito es obtuso

El resultado que se utilizara es la relación del ángulo inscrito con su correspondiente ángulo central, solo que, para este caso, estos ángulos serán especiales: 90° y 180°

Primero, se justifica la construcción de las rectas tangentes a la circunferencia que pasan por un punto exterior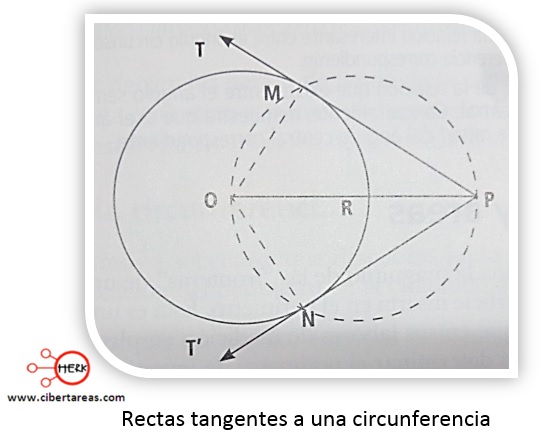

Es importante conocer lo que se debe mostrar para afirmar que las rectas construidas son tangentes a las circunferencias, los argumentos son:

1.- Se trazan los segmentos

2.- Se observa que , que es igual a 180°

3.- , por el teorema del ángulo central e inscrito

4.- , es un ángulo recto

La recta T es tangente al círculo propuesto, se establece un argumento similar para la recta tangente T´

Ahora es importante justificar la construcción delas tangentes exteriores a dos circunferencias dadas. Los pasos para ello se pueden ver realizados en la siguiente figura:

5.- Por el teorema del ángulo central e inscrito, se tiene que este paralelogramo tiene un ángulo recto M, ya que , que vale 180°

6.- Si , entonces el paralelogramo es un rectángulo, lo que implica que M´M´´ es perpendicular a los radios de las circunferencias dadas y, por lo tanto, tangente a ellas, algo similar para en el argumento que se establece para la recta tangente T´