Teorema de los ángulos central e inscrito en una circunferencia en Matemáticas 2
Este teorema nos dice que:
Un teorema es una proposición que necesita ser demostrada, en ella se pueden distinguir dos componentes:
-Hipótesis
-Suposición de algo posible o imposible que se da como cierto
-Tesis
-Proposición que se debe demostrar con razonamientos
Para realizar la demostración, se analizaran cada posición posible de estos ángulos en la circunferencia
Posición 1
-El centro O esta sobre un lado del ángulo inscrito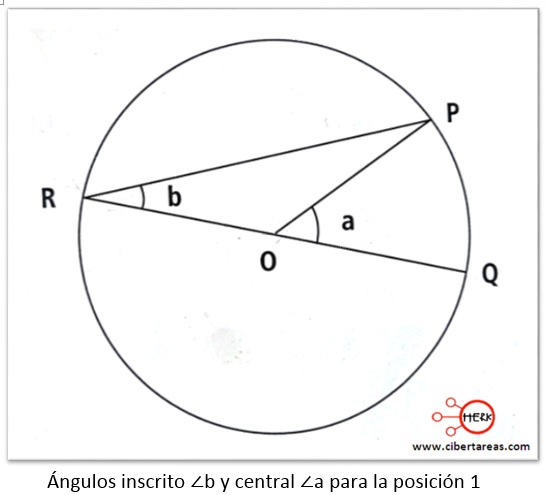
Hipótesis
es su correspondiente ángulo inscrito
Tesis
Demostración
-El sistema de las ecuaciones de los pasos 4 y 5 puede resolverse del siguiente modo:
-Se sustituye la primera ecuación en el lado izquierdo de la segunda:
-En la siguiente imagen se pude observar los ángulos notables, central e inscrito, los cuales están marcado en un campo de béisbol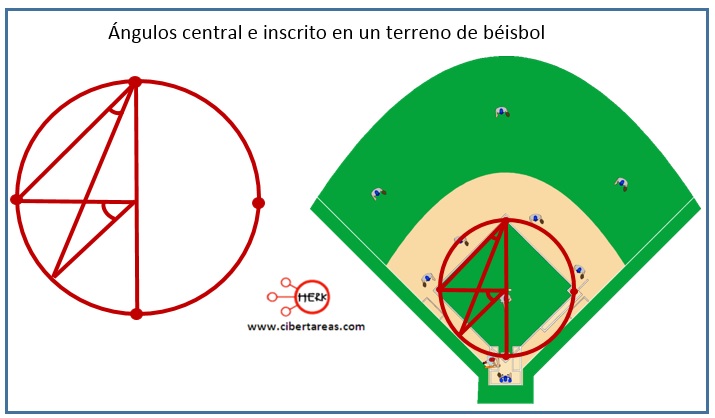
Posición 2
-El centro O está en el interior del ángulo inscrito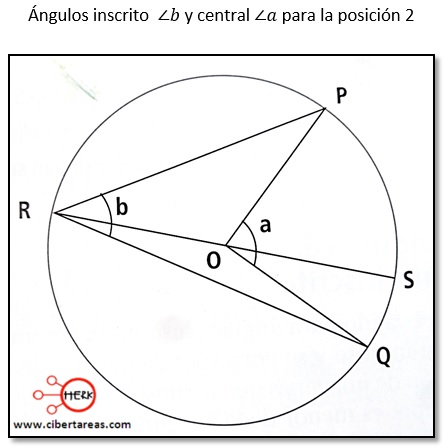
Demostración
-Se basa completamente en la posición 1, lo único que se necesita es trazar el diámetro de la circunferencia 
-Una vez realizado este trazo auxiliar, se podrá observar una construcción geométrica como en la siguiente figura (dos veces):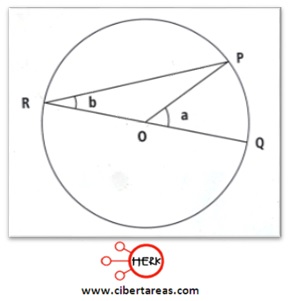
-Otra caracteristica es que los angulos de interes
se ha dividido en dos partes, y para cada uno se cumple la tesis planteada para la posicion 1
-Ademas, la suma de estas partes constituyen, en cada caso, el angulo que no interesa
Posición 3
-El centro O está fuera del ángulo inscrito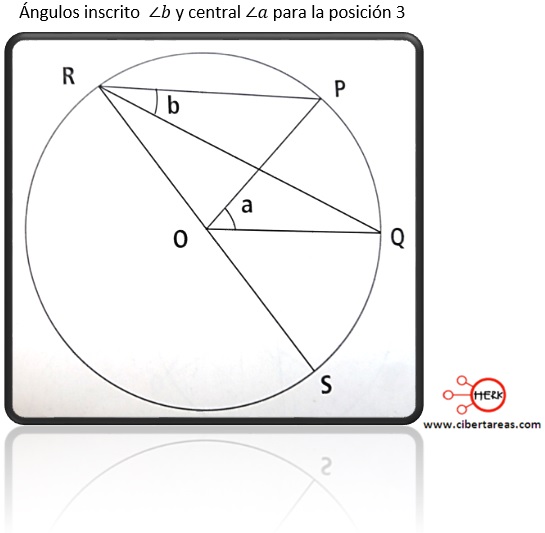
Demostración
-El procedimiento se basa en llevar esta posición a cualquiera de los anteriores ya demostradas
-Para lograrlo, se traza el diámetro de la circunferencia 
-Con este trazo auxiliar, nuevamente se tiene el esquema de la posición 1 (dos veces)
-También los ángulos de interés se obtienen con la aplicación de la tesis para la posición 1
