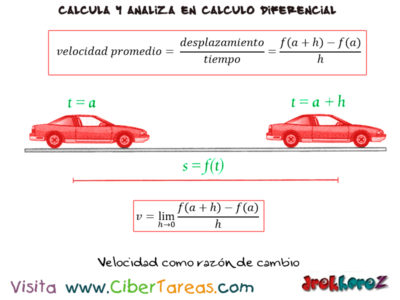
Velocidad como razón de cambio en un periodo de tiempo en Calculo Diferencial, considerado como otra razón de cambio fundamental en el descubrimiento del cálculo diferencial es el límite del valor de las velocidades promedio medidas en periodos cada vez más cortos de un objeto en movimiento.
Si un objeto se mueve en linea recta la ecuación de movimiento que describe es:
s=f(t) donde el desplazamiento desde el punto de partida en el instante (t).
En el intervalo de (t)=a hasta (t)=a el cambio de posición es f(a+h) -f(a).La velocidad promedio por definición es:
Que es lo mismo que la pendiente de la secante PQ de la curva que vimos en la sección anterior.
Cuando hacemos los cálculos de la velocidad promedio en periodos cada vez mas cortos, lo mismo que hacer que [h] tiende a 0 y lo que obtenemos es la velocidad instantánea [v] en el instante (t)=a como límite de las velocidades promedio en la imagen anterior se aprecia la formula.
Esto quiere decir que la velocidad en el instante (t)=a es igual a la pendiente de la recta tangente en el punto P de la curva de posición de un objeto en movimiento.
El siguiente imagen de una gráfica de la función de un móvil en distintos tiempos:
1.- La velocidad inicial del móvil: La velocidad inicial es cero
2.- Donde es mayor la velocidad en B o en C: La pendiente de la tangente es mayor en C que en B por tanto la velocidad es mayor en C.
3.- Dónde aceleraba o desaceleraba el móvil en A y C aceleró en B desaceleró.
4.- Pasó entre D y E ya que el móvil se detuvo en la pendiente es cero.
Otro ejemplo claro es en la siguiente tabla de población [P] representado en miles de una población de una ciudad, desde el año 2005 hasta el año 2015: