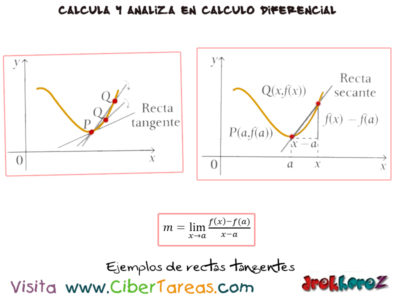
El Proceso para determinar el cambio en Tangentes en el Calculo Diferencial si tenemos una curva que tiene por ecuación y=f(x) y queremos hallar la tangente en un punto dado P(a,f(a)) debemos considerar otro punto cualquiera de la curva Q(x,f(x)) y calcular la pendiente de la recta secante PQ.

Realizamos que x tienda hacia a para que Q se aproxime a P a lo largo de la curva. Cuando esto ocurre, entonces la pendiente m_PQ de la recta secante tiende a la pendiente de la recta tangente como limite y definimos la recta que pasa por P con pendiente m como:

Recta que pasa por el punto P(a,f(a)) de la curva y=f(x) y cuya pendiente es el limite:

Si acercamos en el punto de la tangencial del punto P de una curva con la recta que pasa por él lo que vemos es que en esta posición es donde la curva se parece más a la recta.

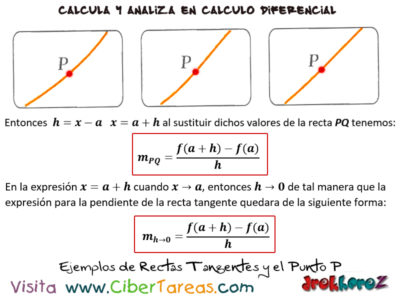
Una forma mas fácil y amigable de expresar la pendiente de la recta tangente a una curva es hacer las siguientes transformaciones.

1.-En la ecuación de la recta tangente a la parábola y=2-x² en el Punto P(1,1). Tenemos que a=1 y f(x)=2-x² asi que la pendiente de la recta tangente es:

2.-En la pendiente m=-2 y el punto de la curva P(1,1) podemos encontrar la ecuación de la recta tangente es decir:

y-1= -2(x-1)
y-1= -2x+2

Simplificando e igualando a cero nos queda:

2x+y-3=0

En la siguiente imagen se muestra la parábola y su tangente en P(1,1):

3.-Si f(x)= 1/x₂ así que la pendiente de la recta tangente P(2,1/4) es:

En la pendiente m=-1/4 el punto de la curva P(2,1/2) podemos encontrar la recta tangente por lo tanto:

y-1/4= -1/4(x-2)

Multiplicando por 4 tenemos:

4y-1=-(x-2)

Simplificando e igualando a cero nos queda:

x+4y-3=0

En la siguiente imagen apreciamos la gráfica muestra la curva su tangente en P(2,1/4):

–