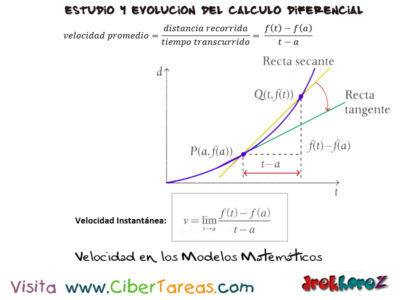
La Velocidad en los Modelos Matemáticos en el estudio del Calculo y su evolución, hay que recordar que en la gráfica de la Tangente comparado con el movimiento de un automóvil que se mueve en línea recta y graficaremos los puntos correspondientes a la distancia recorrida como función del tiempo:

d = f(t)

Después de [t] segundos la velocidad promedio en el intervalo [a,t] es:

Llevando a concluir que es lo mismo que la pendiente de la recta secante. La velocidad cuando [t=a] es el valor límite de la velocidad promedio cuando [t] se aṕroxima mucho a la abscisa [a]. Este límite se llama Velocidad Instantánea v y se representa por la expresión en la de la velocidad instantánea en la imagen anterior.

Gracias al Cálculo Diferencial si resolvemos problemas de la tangente a una función , prácticamente también lo hacemos para diferentes situaciones referentes a [velocidades] o bien a [otras razones de cambio].