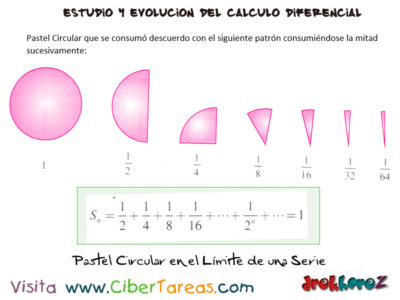
Limite de una Serie en los Modelos Matemáticos en el estudio del Cálculo y su evolución del calculo Diferencial, utilizaremos como ejemplo un Pastel Circular que se consume desacuerdo con el siguiente patrón:
El primer día se come la mitad, al día siguiente la otra mita que queda, al tercer día de nuevo se consume la mitad que queda y así sucesivamente observa la siguiente imagen:
Queda claro que el pastel se va a terminar, en teoría el experimento sugiere que si sumamos la infinidad de fracciones al ir seccionando lo que queda del pastel la “Suma Sn” queda así:
Nos lleva a concluir que si el número de término “n” es suficientemente grande, podemos aproximar la suma “S” tanto como se quiera al número 1 y que es razonable decir que la suma de la serie es infinita es 1.
Conocerme al agregar termino, la suma se aproxima cada vez más a 1. Por tanto la suma de la serie anterior se puede escribir de manera simbólica de la siguiente manera y es de forma mas compacta.
Hay que recordar que “El límite de la suma infinita S cuando “n” tiende a infinito es 1″ con esto consideremos las ideas básicas del limite que son importantes para definir el calculo diferencial e integral