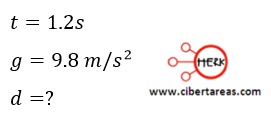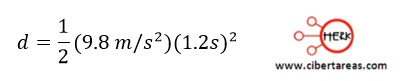Caída libre en Física 1
El movimiento rectilíneo con aceleración constante cuenta con un ejemplo muy común, al cual se le denomina ciada libre, un cuerpo en caída libre se define como:
Hay que considerar que este tipo de movimiento se presenta a menudo en la vida cotidiana, por ejemplo:
-Al dejar caer una moneda al piso
-Cuando una fruta madura se cae del árbol
Sin embargo, debemos saber cuándo la caída libre de un cuerpo es un movimiento rectilíneo con aceleración constante
Haciendo un poco de historia, la caída libre de los cuerpos era un tema de interés, por eso, Aristóteles afirmaba que los cuerpos caían debido a que su lugar natural era el suelo y que hacían todo lo posible para llegar a el, también sostenían que los cuerpos más pesados llegan antes al suelo que los cuerpos ligeros cuando se soltaban simultáneamente desde la misma altura
Posteriormente, Galileo Galilei explico correctamente y en forma matemática la caída de los cuerpos, propuso que:
-Todos los cuerpos, grandes o pequeños, ligeros o pesados en ausencia de fricción (debido a la resistencia del aire), caen en la Tierra con la misma aceleración y con la misma velocidad cuando se sueltan desde la misma altura
Con sus teorías, identificó la caída libre de los cuerpos como un movimiento rectilíneo vertical con aceleración constante, por lo que surge el siguiente concepto, aceleración de la gravedad
– La magnitud al nivel del mar de g es de 9.8 m/s2, su dirección es vertical con sentido hacia abajo (centro de la tierra)
-El valor de g en la Tierra varía según la altitud y la región donde se mida, ejemplo: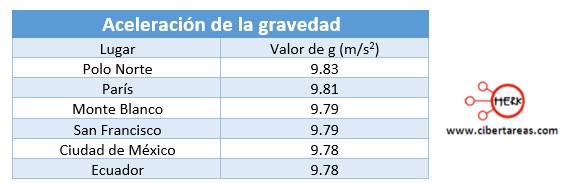
Actualmente para estudiar la caída libre de los cuerpos se recurre a la fotografía estroboscópica, la cual consiste en tomar una fotografía con una exposición larga de un suceso iluminado con una lámpara (estroboscopio) que emite luz a intervalos regulares de tiempo y de muy corta duración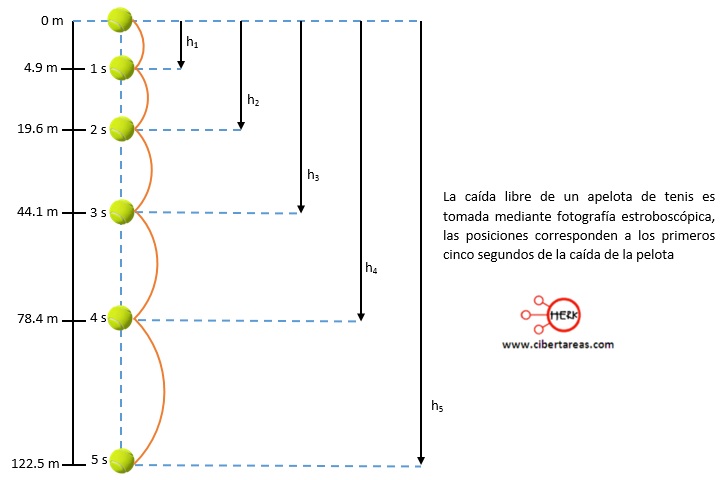
En la figura anterior se puede observar que los desplazamientos de la pelota aumentan conforme el tiempo pasa, en este caso las imágenes de la pelota fueron tomadas cada segundo
La gráfica del desplazamiento o distancia recorrida contra el tiempo de la pelota de tenis, es una parábola: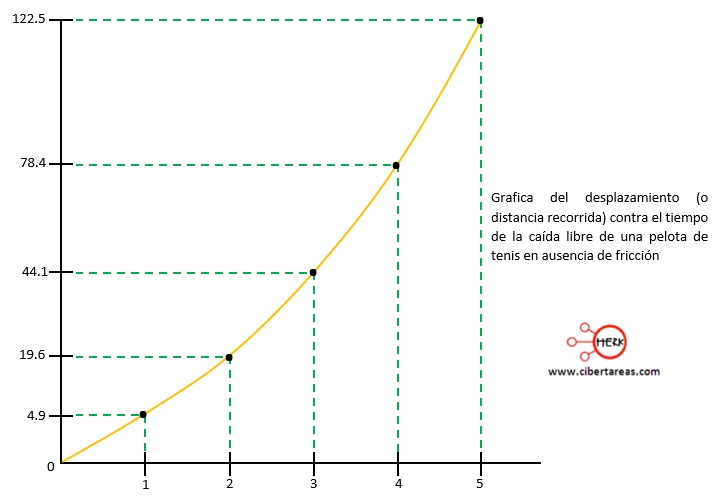
La grafica anterior es característica del movimiento rectilíneo con aceleración constante, para este ejemplo, la velocidad aumento a cada instante, se dice que el movimiento es uniformemente acelerado
Si se efectúa el cociente d/t2 para cada uno de los valores que aparecen la imagen de la caída libre de la pelota de tenis, y se registran en la siguiente tabla: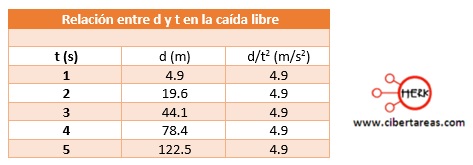
Con lo anterior se pude observar dicho cociente es constante e igual a 4.9 m/s2, es decir:
O lo que es lo mismo:
Si se compara esta expresión con la ecuación de la gráfica anterior, distancia-tiempo, se encuentra que la aceleración de la caída libre de la pelota de tenis es 9.8 m/s2, es decir:
Por tanto
Ya que la aceleración se representa por g se tiene entonces que g = 9.8 m/s2
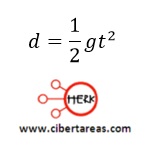
Esto significa que la ecuación que relaciona la distancia que recorre un cuerpo en caída libre con el tiempo que emplea en recorrerlo está dada por:
El hecho de que la aceleración sea 9,8 m/s2 significa que el cuerpo en caída libre incrementa el valor de su velocidad 9,8 m/s cada segundo, como se muestra en la siguiente imagen: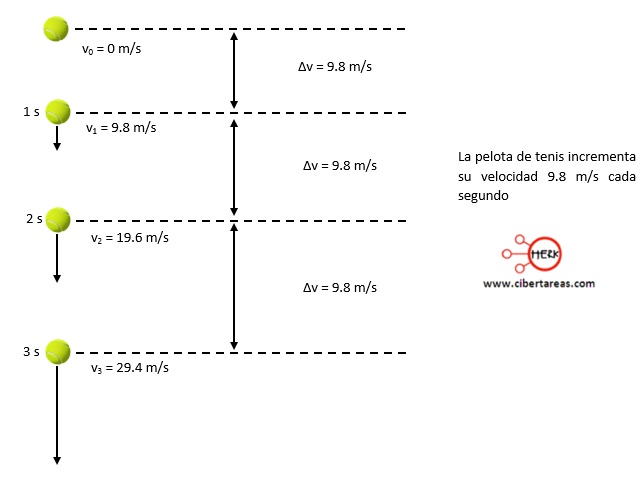
Tenemos que las mismas ecuaciones que se tienen para describir el movimiento rectilíneo de un cuerpo con aceleración constante sirven para describir el movimiento de caída libre de un cuerpo, con las diferencias de que en este caso la aceleración se representa por g y que la velocidad inicial es cero
La siguiente tabla muestra las semejanzas y diferencias de las ecuaciones
Ejemplo:
Problema
-Una vaca se cae de un puente que cruza por encima de un rio y golpea el agua 1.2s después
– ¿Cuál es la altura del puente sobre el rio?
Solución
-Datos
-Formula
-Como se trata de caída libre se utiliza:
-Sustitución
-Resultado
