En la Integración Aproximada en Cálculo Integral ya existen dos situaciones en las cuales es imposible hallar el valor exacto de una integral definida. La primera se presenta cuando no tenemos manera de conocer una antiderivada f(x). Por ejemplo es imposible evaluar con exactitud la siguiente integral.
En la Segunda sugiere cuando dicha función se determina con la experimentación al recolectar los datos a través de lecturas de instrumentos , esto da la posibilidad que no haya formula para la función. Ya que cualquiera de los casos conveniente usar algún método de integración que tenga como referente “Sumas de Riemann” uno de ellos es la regla de los trapecios.
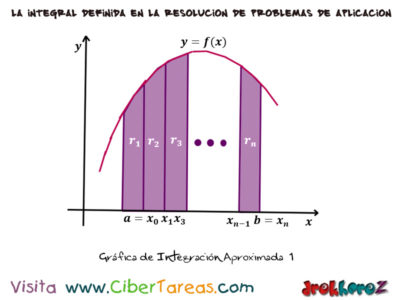
Logrando comprender mejor esta situación, analicemos la siguiente figura y designemos como es el [A] área bajo la curva cuya función es y=f(x), el eje de las x y las ordenadas x=a y x=b.
[rn]= área de la región respectiva de cada uno e los trapecios dibujados y cuya suma es el área [A].
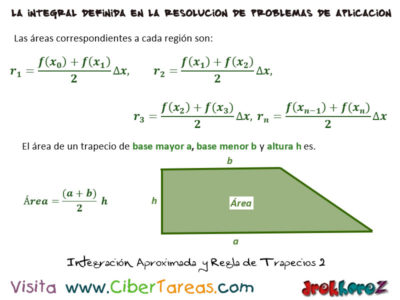
Se destaca que las figuras geométricas que suman el área [A] de Aproximación bajo la curva no son rectángulos de Riemann sino Trapecios y si recordamos que el área de un trapecio se obtiene con l semisuma de sus bases por la altura, entonces las áreas correspondientes a cada región son:
El Área de un trapecio de base mayor [a], Base menor [B] y Altura [h], entonces el [A] área bajo la curva es la suma de las regiones es decir, que al sustituir tenemos las siguiente imagen:

Al factorizar Δx y realizamos la suma de los términos semejantes , el área [A] apreciable en la imagen, ya que la expresión nos enseña que cuantos más trapecios consideremos Δx tiene de a 0. n-> infinito y nuestra aproximación sera más precisa.