Las Funciones Crecientes y Decrecientes variables en producciones, máximos y mínimos en cálculo diferencial analizar si las funciones son crecientes o decrecientes y observemos es la pendiente o derivada en cada punto de las gráficas.
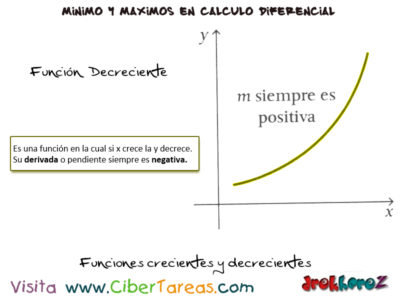
1.- Función Decreciente: Es una función en la cual si x crece la y decrece. u derivada o pendiente siempre es negativa.
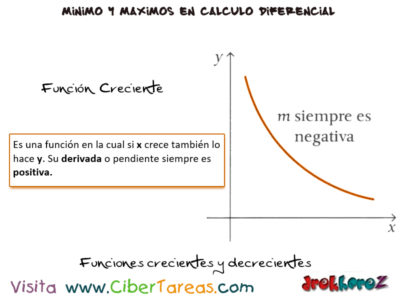
2.-Función creciente: es una función en la cual si x crece también lo hace y su derivada o pendiente siempre es positiva.
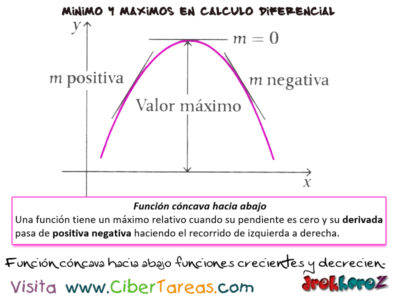
En los conceptos de funciones creciente y decreciente de las gráficas anteriores al analizar la concavidad de una curva, veremos que una curva concava hacia abajo, sin lugar a duda tiene un valor máximo, además su derivada cambia de positiva a negativa es decir decrece.
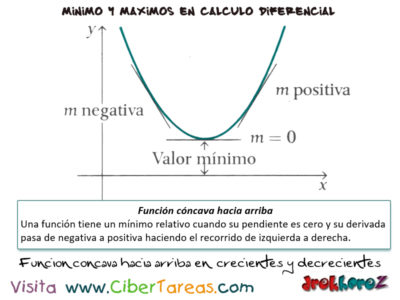
En una curva cóncava hacía arriba tiene un mínimo y la derivada cambia de negativa a positiva, es decir crece.La idea nos da la pauta para encontrar un criterio que nos garantice como encontrar los valores extremos de una función.
1.-Función cóncava hacia abajo: Una función tiene un máximo relativo cuando su pendiente es cero y su derivada pasa de positiva a negativa haciendo el recorrido de izquierda a derecha.
2.-Función cóncava hacia arriba: Una función tiene un mínimo relativo cuando su pendiente es cero y su derivada pasa de negativa a positiva haciendo e recorrido de izquierda a derecha.
Podemos formular el primero método para calcular los máximos mínimos relativos de una función y=f(x).