Los Relativos con el criterio de la primera derivada en máximos y mínimos – Cálculo Diferencial

Como criterio de la primera derivada para calcular los máximos y míimos relativos de una función.

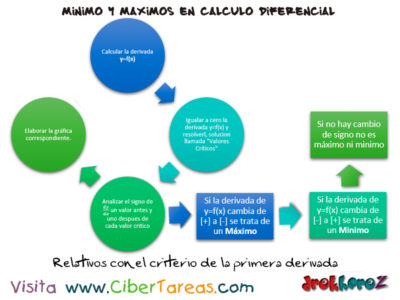
1.- Calcular la derivada de y=f(x)

2.-Al igualar a cero la derivada de y=f(x) y resolver la ecuación, estas soluciones se omitir algunos valores críticos.

3.-Analizar el siglo de dy/dx un valor antes y uno después de cada valor crítico sin omitir alguno de ellos.

3.1.- Si la derivada de y=f(x) cambia de (+) a (-) se trata de un Máximo.

3.2.- Si la derivada de y=f(x) cambia de (-) a (+) se trata de un Mínimo.

3.3 Si no hay cambio de signo no es ni máximo ni mínimo.

4.- Elaboración de la gráfica correspondiente.