Otras formas de indicar la derivada en el Calculo Diferencial,si partimos de la notación de función y=f(X) para recordar que x es la variable independiente y la dependiente es y otros símbolos para escribir la derivada son:

“La derivada de f(X) respecto a x”
No se debe considerase como una división deben verse sólo como “Operadores de Derivación“.

Una función f es diferenciable en a sólo si f'(a) existe,en general son tres situaciones en que una función y=(x) deja de ser diferente.

Un ejemplo claro es en la función y=[x] no es diferenciable en x=0 porque f'(0) no existe:

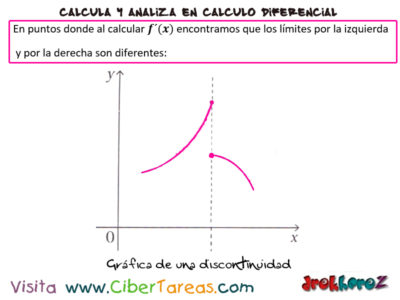
Como en el Limite por la izquierda y por la derecha de cero son diferentes, entonces f'(0) no existe. En la inexistencia geométrica de f'(0) podemos verla en la siguiente gráfica:

a) En puntos donde al calcular f(x) encontramos que los límites por la izquierda y por la derecha son diferentes.

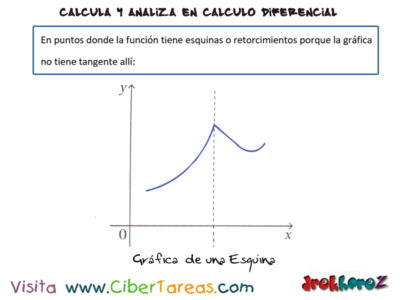
b) En puntos donde la función tiene esquinas o retorcimientos por que la gráficas no tiene tangente allí.

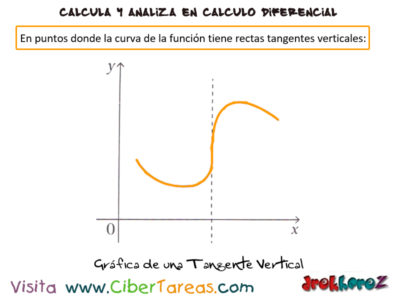
c) En puntos donde la curva de la función tiene rectas tangentes verticales.