La Derivada como función en el Cálculo Diferencial, si hacemos que el número a varíe y lo reemplazamos con la variable x entonces la expresión de la derivada f(X) va quedar como.

En el dominio de f(x) es el conjunto de numeros x tal que la derivada de f existe, la definición simbólica de la derivada de una función f(x) se lee como:

“El límite de la relación del cambio de la variable dependiente al cambio de la variable dependiente al cambio de la variable independiente cuando este último tiende a cero”.

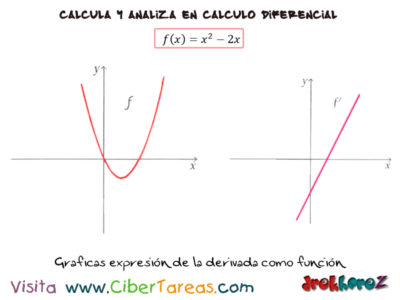
Un ejemplo claro es si f(X)=x² – 2x encuentra la derivada f'(X) como función de x. Traza las gráficas de f(x) y f'(x) para compararlas y explicar su significado.

Al comparar las gráficas debemos recordar que la derivada f’ representa la pendiente de la recta tangente a f en cada punto. Por ejemplo observa que f'(x)=0 cuando f tiene una pendiente horizontal [en x=1] y que f'(X) es negativa (x<1) o positiva (x>1) cuando f tiene pendientes negativa o positiva respectivamente:

Un ejemplo claro es si f(x) = 2√x
encuentra la derivada fx) como función de x:

Aplicando la definición de derivada tenemos que:

La derivada de f(x) es f'(x)=1/√x y existe sólo para x > 0.