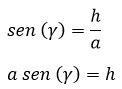Ley de cosenos en Matemáticas 2
Para este tema se aplicara la fórmula de los cosenos en una actividad recreativa, por ejemplo:
-José está jugando en una resbaladilla del parque, durante su descenso se encuentra en el punto B, es necesario determinar la distancia que le falta para llegar al punto C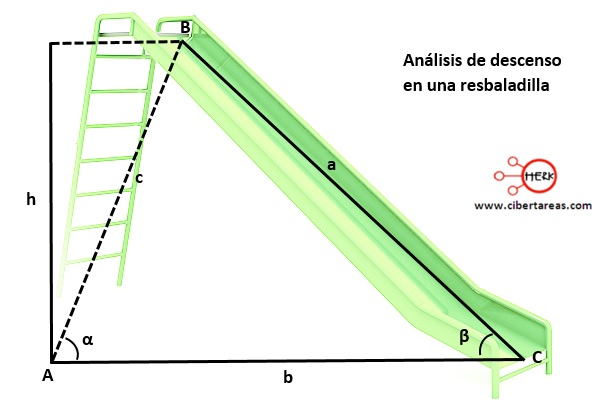
Solución
-Datos
h
Altura a la que se encuentra el individuo al momento de empezar a deslizarse
a
Distancia entre el individuo y el final de la resbaladilla
Angulo que marca el punto de deslizamiento del individuo
b
Distancia entre las bases de la escalera y la resbaladilla
Angulo de elevación desde la base de la resbaladilla
-Análisis
Si el problema hubiera implicado solo los referentes d, h y c, como se muestra la siguiente figura, la solución se habría alcanzado con el teorema de Pitágoras
Sin embargo, no siempre puede tener un triángulo rectángulo en los modelos matemáticos para solucionar problemas
Por eso se deben usar herramientas más sofisticadas
Este problema se reduce a resolver el ∆ABC de la siguiente figura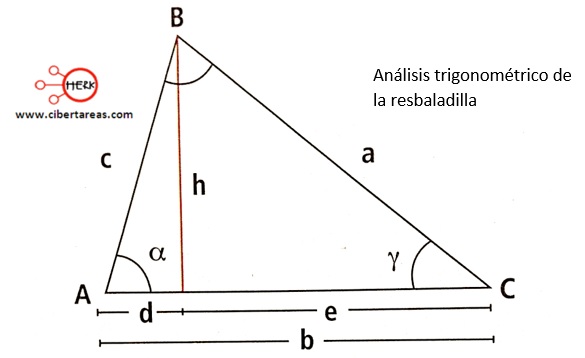
La altura h permite observar algunas propiedades:
Los triángulos de lados d, c, h y h, a, e son rectángulos, por lo que utilizando el teorema de Pitágoras se pueden calcular h y e en términos de a
Para obtener h, tenemos que recurrir a la función seno:
Ahora se obtiene la distancia de e:
Para el triángulo rectángulo de lados d, c, h, se cumple:
Y como se sabe que h = a sen![]() , entonces:
, entonces:
Al retomar el concepto de identidades pitagóricas, se puede emplear la siguiente fórmula:
Por tanto:
Al acomodar esta ecuación se define la ley de cosenos:
Entonces, para calcular la distancia que le falta recorrer al individuo de la resbaladilla, se tienen que encontrar el valor de a, lo que implica despejar esta variable de la fórmula de la ley de cosenos y formar finalmente una ecuación cuadrática en términos de a:
-Síntesis interpretativa
Esta es una de las aplicaciones de la ley de cosenos
Ejemplo
-Es necesario encontrar la longitud del tercer lado del siguiente triangulo mediante le uso de la ley de cosenos
Solución
-Datos
Lado a = 7.42 cm
Lado x = ¿?
Hipotenusa = 11.48 cm
-Análisis
Es necesario utilizar la ley de cosenos:
Ahora lo siguiente es asignarle a la formula las variables de este ejemplo: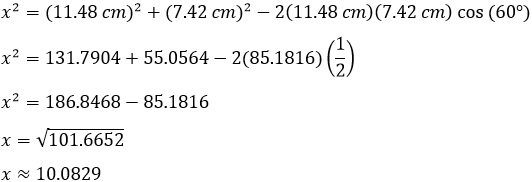
-Síntesis interpretativa
Con la ayuda de la ley de cosenos se ha encontrado el valor del cateto