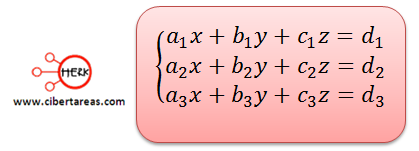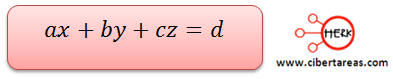Sistemas de ecuaciones simultaneas de tres ecuaciones con tres incógnitas – Matemáticas 1
Lo primero que tenemos que considerar es el conocer los procesos algebraicos que emplean determinantes para resolver sistemas de ecuaciones, esto nos ayudara y conducirá a desarrollar problemas que se presentan en la vida cotidiana y resolverlos de acuerdo con sus planteamientos.
Comúnmente las ecuaciones de primer grado con tres variables se trabajan en conjuntos forados por agrupaciones de este tipo de ecuaciones.
Por último se requiere buscar el punto que las satisface de manera simultánea.
Este sistema representa tres planos en el espacio, para encontrar la solución a un sistema de ecuaciones lineales con tres incógnitas equivaldría a encontrar las coordenadas del punto de intersección (x, y, z) de tres planos en el espacio, en el caso que existiera un punto.
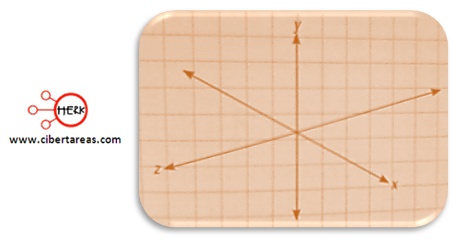
Para graficar este tipo de sistema de ecuaciones se representa con un modelo de tres dimensiones.
Un plano en el espacio puede ser representado con una hoja de papel
Si se diera el caso de tener dos planos, en otras palabras dos hojas de papel, es conveniente considerar ¿Qué posiciones podría haber entre ellas? Los planos son ajenos y paralelos
Podemos afirmar que los planos son idénticos ya que coinciden en todos sus puntos
Los planos son ajenos y no paralelos
Vamos a hacernos las siguientes preguntas:
¿Qué sucede si tenemos tres planos?
¿Cuántas posiciones pueden establecerse entre sí?
Existe un caso en que los tres planos se intersecan en un punto:
Aunque el grafico lo sugiere, los planos no necesariamente deben ser perpendiculares entre sí, lo que interesa averiguar es que condiciones sucede esto.
Con esto sabemos que una ecuación de la forma:
Esta ecuación es la representación algebraica de un plano en el espacio tridimensional.