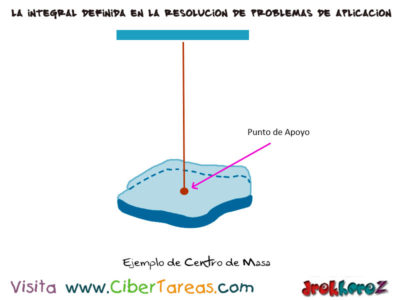
El Centro de Masa en Calculo Integral, la idea central de esta sección es encontrar el punto de apoyo para que la masa de un cuerpo se equilibrio horizontalmente. Dicho punto se llama centro de masa o centro de gravedad que se puede apreciar en la siguiente imagen
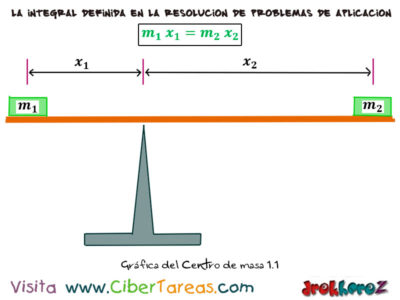
Un ejemplo claro al experimentar una barra de peso despreciable y cargamos dos masas [m1 y m2] en lados opuestos del punto de apoyo [fulcro] a distancias [x1 y x2] respectivamente, la barra igual que una balanza se equilibra cuando:
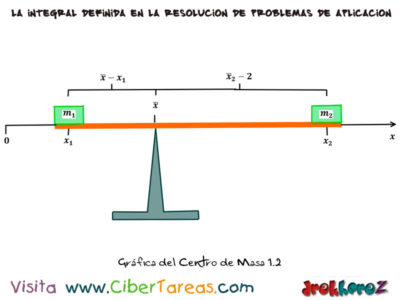
Gráficamente se aprecia en la imagen anterior, pero si hacemos considera la barra del experimento anterior con el eje y le asignamos la coordenada x al punto de apoyo entonces el resultado es el siguiente:
Fácilmente la ecuación de equilibrio en estas circunstancias queda así, al agrupar los términos que tienen [x] y resolvemos la ecuación para esta variable que obtenemos es el centro de masa del sistema con respecto al origen de coordenadas es decir:
Para los términos m1 x2 y m2x2 se conocen como los momentos de masa de m1 y m2 respectivamente. Se puede comprobar que si se tienen [n] partículas en el plano cartesiano con masas m1, m2… mn y posicionamos en los puntos (x1,y1), (x2,y2)….(xn,yx) respectivamente, generalmente el momento del sistema respecto del eje y tendencia a girar en tono a y es decir,
Que además del momento del sistema con respecto al eje x el cual tienen tendencia al girar en torno a x es decir. Por lo tanto las coordenadas de masa (x,y) del sistema en el plano cartesiano así: