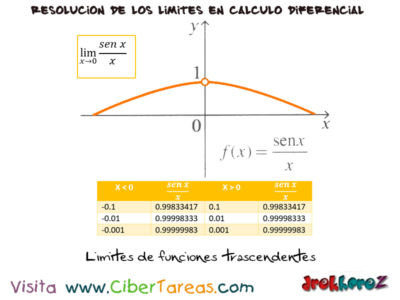
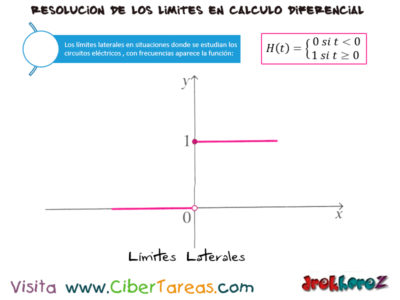
Los Límites de funciones trascendentes en Calculo Diferencial para encontrar el Limite de senx.
Tomare como ejemplo clara la función f(x) = senx/x no está definida en x = 0, pero podemos construir una tabla para valores próximos a 0. Recuerda que cuando calculemos senx, la calculadora debe estar en la modalidad de radianes:
Los Límites de funciones racionales en el Cálculo Diferencial en aproximaciones numéricas, cuando una función no se encuentra definida para uno o más valores.
La manera más amigables de conocer sin un limite existe es utilizar las tablas de aproximación numérica que hemos utilizando hasta ahora, existe casos excepcionales en que no nos conducen a la respuesta correcta pero estos o los trataremos aquí.
Los Límites Laterales en Cálculo Diferencial, en situaciones donde se estudian los circuitos eléctricos, con frecuencia aparece la función que sirve para describir una corriente eléctrica que hace circular en el instante (t=0) y se llama función de “Heaviside”. La siguiente figura muestra su representación gráfica:
La Aplicación de Límites en el Cálculo Diferencial, un ejemplo claro es la resolución del desplazamiento de un automóvil que se mueve en línea recta se expresa con s(t)=9t+t2 donde se mide en segundos y s(t) en metros.
Qué tan lejos viajará en 7 segundos, su desplazamiento después de 7 segundos basta con evaluar s(t) en t=7.
En dicho caso vamos a calcularlo como la función no está defendida para t=7 tenemos que recurrir a una factorización elemental de tal modo:
Los Límites de funciones racionales en Cálculo Diferencial, en la forma r(X)=P(x)/q(x) debemos tener en encuentra que r(x) no está definida para q(x)=0 “Recuerda que la división entre entre cero es indefinida”.
Sin embargo en el cálculo de los límites eso puede ser trivial ya que la definición dice que consideremos los valores de x cercanos a (a) pero diferente de (a).
Al calcular la unción no siendo definida para (x=2) sí lo está cerca de 0 observa la gráfica de la siguiente figura.
