Integración por Partes, Indefinida y Definida en Cálculo Integral, formulario que se puede apreciar en la siguiente imagen:
Etiqueta: calculo integral
El Cálculo de Volúmenes – Cálculo Integral
El Calculo de Volúmenes en Cálculo Integral, en secciones paralelas en elementos de secciones, de la misma forma que se realiza con el área de regiones planas, aquí se utilizara las Integrales Definidas para encontrar los volúmenes de ciertos sólidos en tercera dimensión.
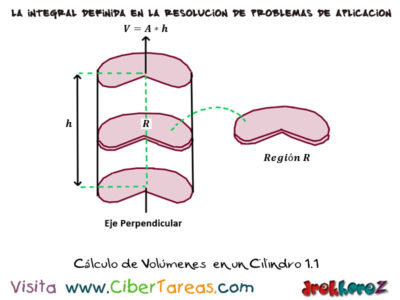
Un cilindro cualquiera con Sección Transversal [R] es un sólido formado por las traslación de la región [R] a largo de un “Eje Perpendicular” a ésta. Si [A] es el área de la región [R] y ésta se traslada a lo largo de una distancia [h] entonces el volumen generado por la sección es V= Axh como se muestra en la siguiente imagen:
Ejemplo sobre la Regla de Simpson – Cálculo Integral
Regla de Simpson – Cálculo Integral
La Regla de Simpson en Cálculo Integral es una opción para la integración aproximada, cuya demostración se omitirá para fines prácticos, esta aproximación se planteaba partir del uso de parábolas en lugar de segmentos rectilíneos.
Dicha regla de Simpson [1710-1761] al aplicar la regla es importante fijarse en el patrón de los coeficientes de esta:
Ejemplos de Integración Aproximada – Cálculo Integral
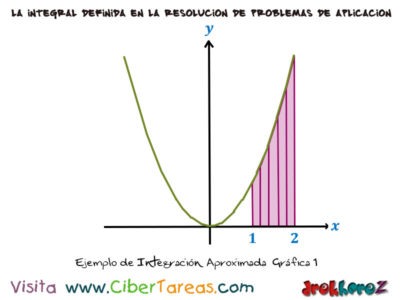
Ejemplo de Integración Aproximada en Calculo Integral, con imágenes y Gráficas que se aplica la regla de los trapecios con [n=5] para obtener una aproximación de la integral, con solución de n=5 ,a=1 , b=2 tenemos así:
A la hora de calcular por medio de la integración defina que se muestra en la imagen anterior.