El Calculo de Volúmenes en Cálculo Integral, en secciones paralelas en elementos de secciones, de la misma forma que se realiza con el área de regiones planas, aquí se utilizara las Integrales Definidas para encontrar los volúmenes de ciertos sólidos en tercera dimensión.
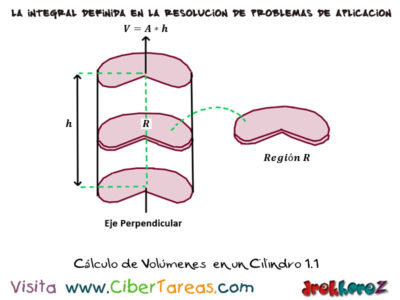
Un cilindro cualquiera con Sección Transversal [R] es un sólido formado por las traslación de la región [R] a largo de un “Eje Perpendicular” a ésta. Si [A] es el área de la región [R] y ésta se traslada a lo largo de una distancia [h] entonces el volumen generado por la sección es V= Axh como se muestra en la siguiente imagen: