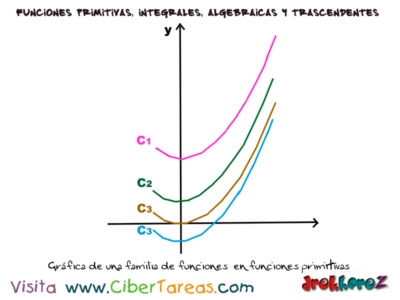
Funciones Primitivas en Calculo Integral, en matemáticas las operaciones tienen sus inversas; por ejemplo para la adicción es la substracción, para la multiplicación es la división, para elevar a una potencia es extraer una raíz etc.
En el calculo integral sucede exactamente lo mismo.
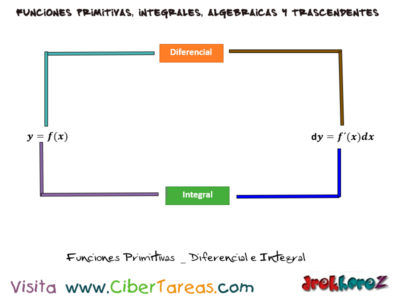
En la integración es la operación que se realiza para obtener la función primitiva f(x) o antiderivada de una expresión diferencial dada, la cual recibe el nombre de integral. La integral es una operación inversa a la derivación, en calculo diferencial aprendimos que si y = f(x) , entonces la derivada de la función es dy/dx= f´(x), o bien si empleamos diferencial, la función es:
El problema fundamental de calculo integral depende de la operación inversa a la diferenciación, es decir: hallar una función primitiva y= f (x), cuya diferencial dy=f´(x)dx es conocida podemos resumir lo que se acaba de exponer con la ilustración siguiente:
La condición que debemos caracterizar a dy para que admita la Función Primitiva sobre un intervalo es que debe tener continuidad en el intervalo. La Función Primitiva f(x) que así se obtiene se llama Integral o Antideriva de la expresión diferencial; el procedimiento para hallarla se llama integración y la operación se indica escribiendo el signo integral [] delante de la expresión diferencial de manera que: