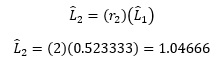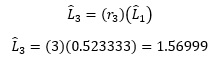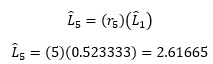Funciones trigonométricas en el círculo unitario en Matemáticas 2
A través del tiempo, el circulo ha sido objeto de razonamientos filosóficos, en este artículo abordaremos un circulo que se caracteriza por tener un radio de longitud 1
En la siguiente figura se muestra tres cicrulos concéntricos son segmento que conforma un ángulo de 30° con respeto al eje x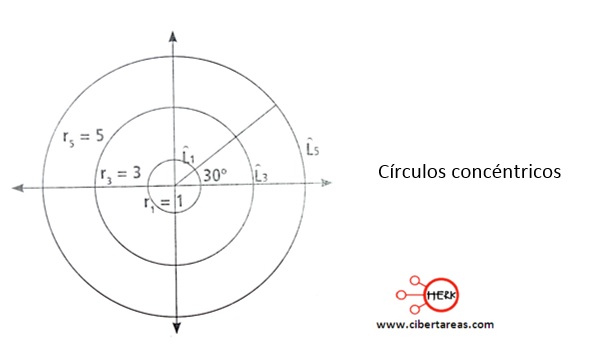
Los radios respectivos con:
r1 = 1
r3 = 3
r5 = 5
Ahora es posible calcular la longitud de arco correspondiente al ángulo de 30° en cada una de las tres circunferencias:
Solución:
Datos
r1 = 1
r3 = 3
r5 = 5
Análisis
Para la longitud de arco con r1 = 1, al sustituir en 
y considerando π = 3.14, se obtiene:
Antes de calcular la longitud de arco para r3 = 3 y r5 = 5, es necesario calcular la de un circulo de r = 2 con el mismo ángulo, esto permitirá obtener un dato de referencia muy útil
Es importante observar que este mismo cálculo se pude realizar a través de la longitud de arco de 
:
Por lo tanto, para calcular las longitudes de arco 
se puede decir:
Para el siguiente tenemos:
Síntesis interpretativa
A partir de 
es posible hallar cualquier longitud de arco
