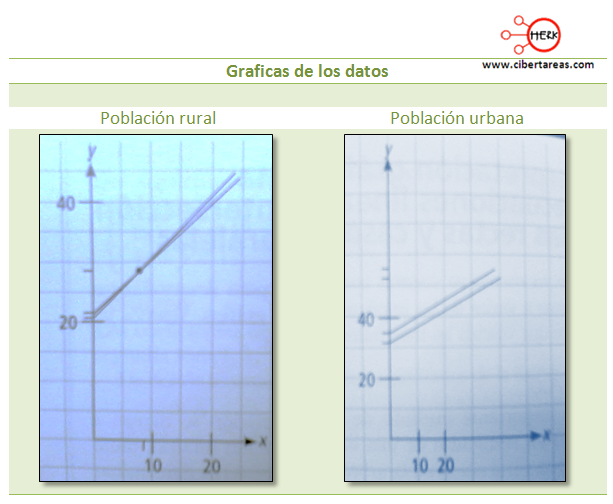
Interpretación grafica de un sistema de ecuaciones lineales: Punto de intersección de las rectas y casos en que son paralelas.
Vamos analizar un ejemplo en el cual se vincula las matemáticas y los análisis estadísticos.
En una clínica de nutrición, se publicaron los resultados de una investigación aplicada a los niños, ubicados en las zonas rurales como el la urbana. Uno de los estudios realizados a los niños, trata de determinar si la obesidad es más común en los niños que en las niñas o de igual manera en los dos géneros.
Tenemos que hacer notar que el índice de masa corporal (IMC) se define entre 18.5 y 25, pero si es mayor o igual a 30 nos indica que existe obesidad.
Analicemos la siguiente información y las respectivas gráficas, con esto vamos a determinar el sistema de ecuaciones lineales que presentan un punto de intersección de las rectas o el caso de rectas paralelas.
Analicemos la solución:
Al sustituir los valores de “y” en cada una de las ecuaciones podemos identificar cómo se van trazando las rectas en cada uno de los casos. Al tomar un valor de 28 para “y” en la población rural tenemos los siguientes resultados:
Con estos resultados, tenemos que el par ordenado es (8, 28), el cual es el punto de intersección de las rectas.
La grafica que se mostró anteriormente indica que los índices de masa corporal coinciden en cierta edad entre niños y niñas de la población rural, y tenemos que en la población seleccionada para el estudio de la zona urbana nunca coincidirán, lo cual se reconoce por las rectas paralelas.