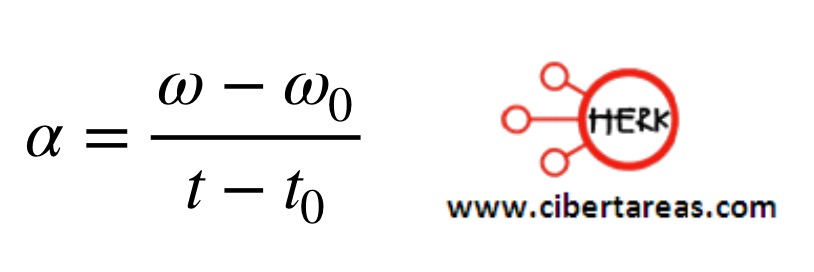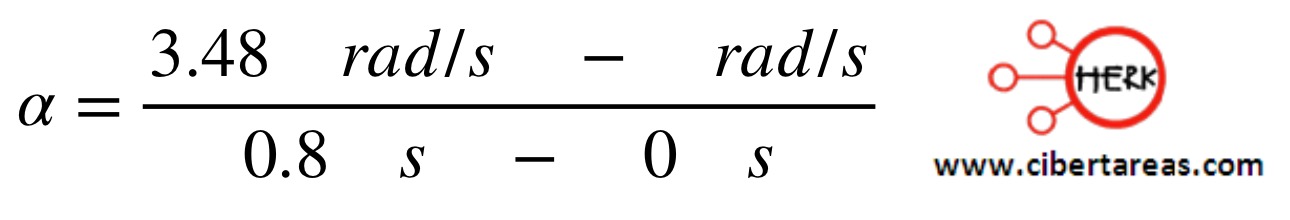Movimiento circular uniformemente acelerado en Física 1
Es importante señalar que cuando un motor se conecta a la energía eléctrica, el eje aumenta su velocidad angular uniformemente desde cero hasta alcanzar cierto valor, para esto transcurre un tiempo determinado
Entonces podemos decir que el eje del motor tiene una aceleración angular
Existen muchos casos casos de aceleración angular, por ejemplo:
-Un CD (disco compacto) incrementa su velocidad angular de manera continua hasta alcanzar la velocidad angular de funcionamiento
Cuando la magnitud de la velocidad angular cambia de un valor inicial ω0 en el instante t0 a un valor final ω en el instante t, la magnitud de la aceleración angular se define como:
Matemáticamente, se calcula por: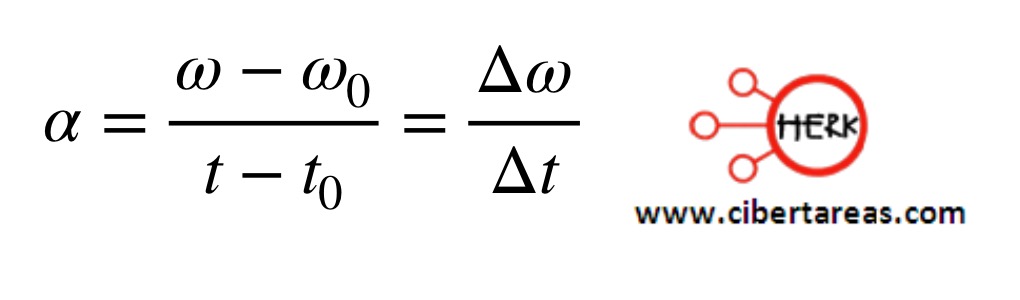
En donde:
𝛼 = magnitud de la aceleración angular
𝛥𝜔 = magnitud del cambio de la velocidad angular
𝛥t = t – t0 = tiempo transcurrido
Si 𝜔0 se da en el instante t0 = 0 s, la ecuación anterior se convierte en:
La unidad de la aceleración angular en el SI es el rad/s2, cuando un móvil tiene una aceleración angular de 4 rad/s2, significa que la magnitud de la velocidad angular del móvil que gira cambia 4 radianes por segundo durante cada segundo de aceleración
Ejemplo del movimiento circular uniformemente acelerado
Problema:
-La tornamesa de un toca discos acelera desde el reposo hasta alcanzar una rapidez angular de 33.3 rev/min en 0.8 s
-¿Cuál es el valore su aceleración angular?
Solución
-Como primer paso se debe de convertir las rev/min en rad/s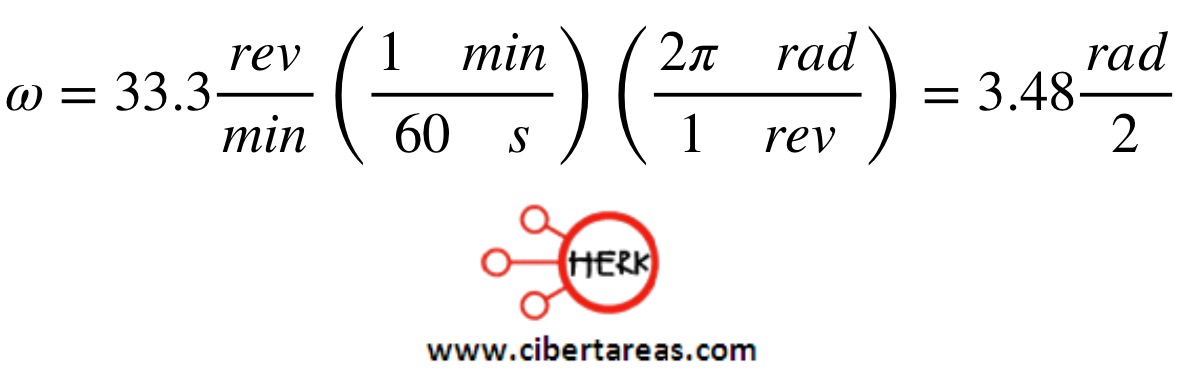
Datos
t0 = 0 s
𝜔0 = 0 rad/s
T = 0.8 s
𝜔 = 33.3 rev/min
Resultado
𝛼 = 4.35 rad/s2
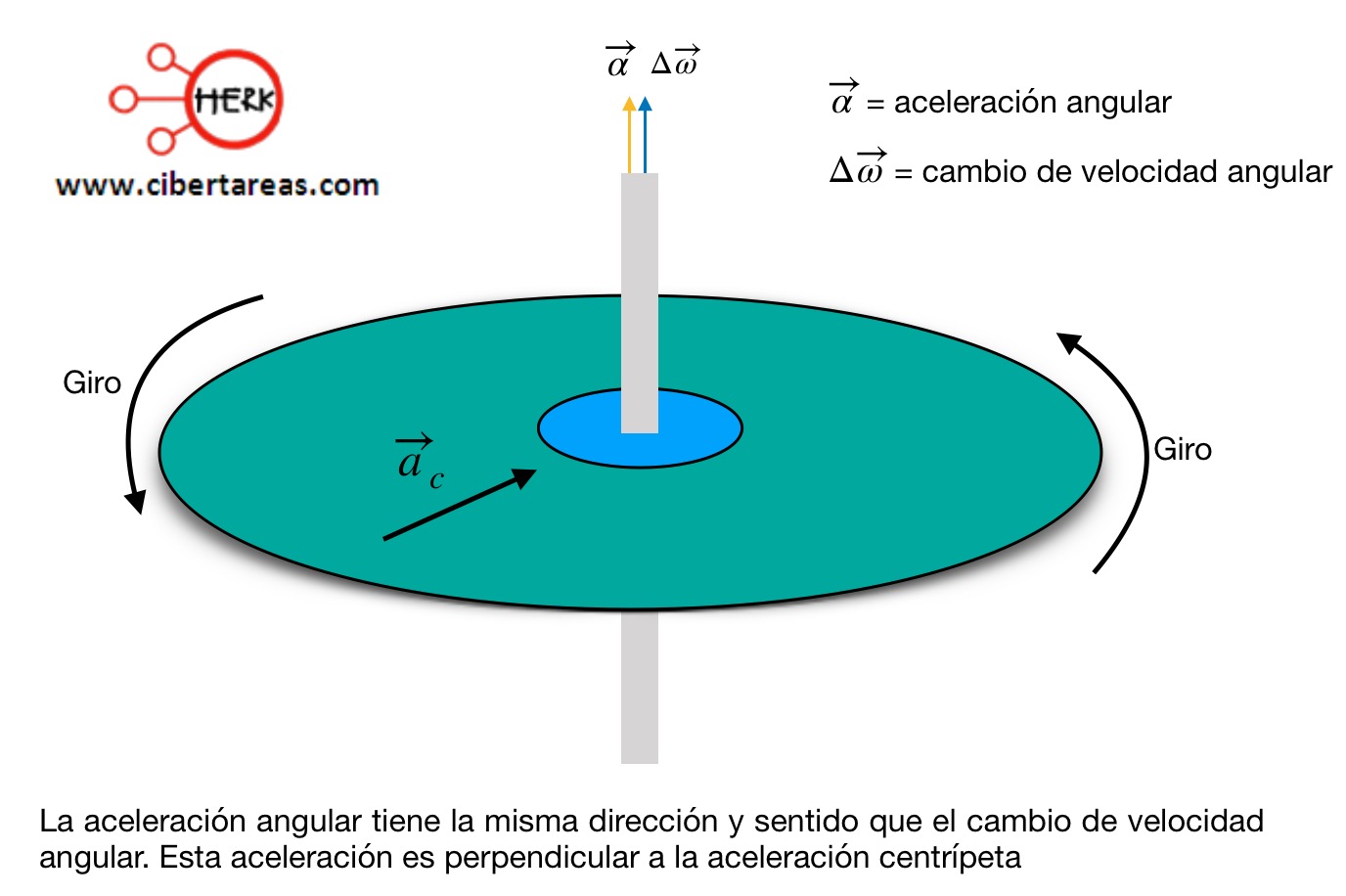
La aceleración angular es una magnitud vectorial que tiene la misma dirección y sentido que el cambio de velocidad ![]() , como se muestra en siguiente figura
, como se muestra en siguiente figura
Al igual que en el movimiento rectilíneo (o lineal), el movimiento circular puede ser uniformemente acelerado (MCUA) o retardado (MCUR)
Para el primer caso la velocidad angular aumenta uniformemente y en el segundo caso disminuye de manera uniforme, en ambos movimientos la aceleración angular es constante
Dadas las semejanzas entre los movimientos circulares (rotacionales o angulares) y rectilíneo, en el siguiente cuadro comparativo se muestran los símbolos empleados para representar las variables que describen las características de un cuerpo en movimiento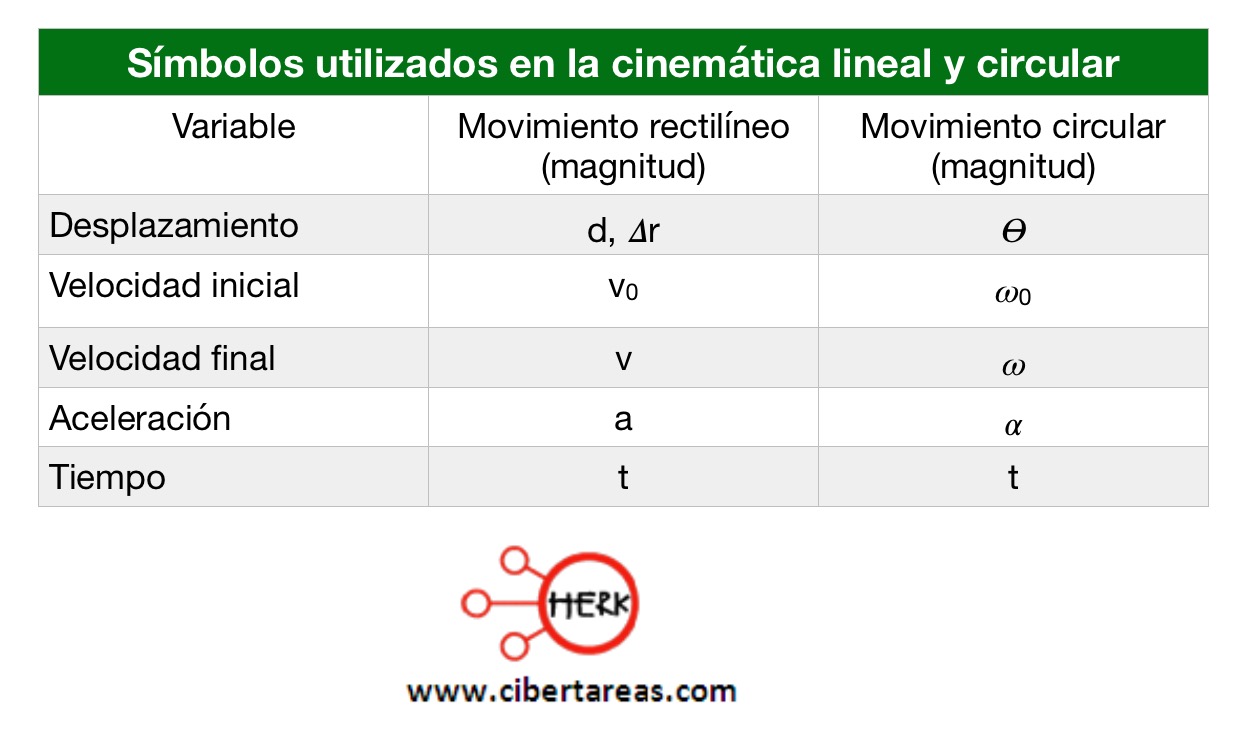
Las semejanzas entre el movimiento rectilíneo con aceleración constante y el movimiento circular con aceleración angular constante permiten obtener por analogía las ecuaciones necesarias para el estudio del movimiento circular con aceleración angular constante
La siguiente tabla muestra las semejanzas entre las ecuaciones del movimiento rectilíneo y del movimiento circular (o rotacional)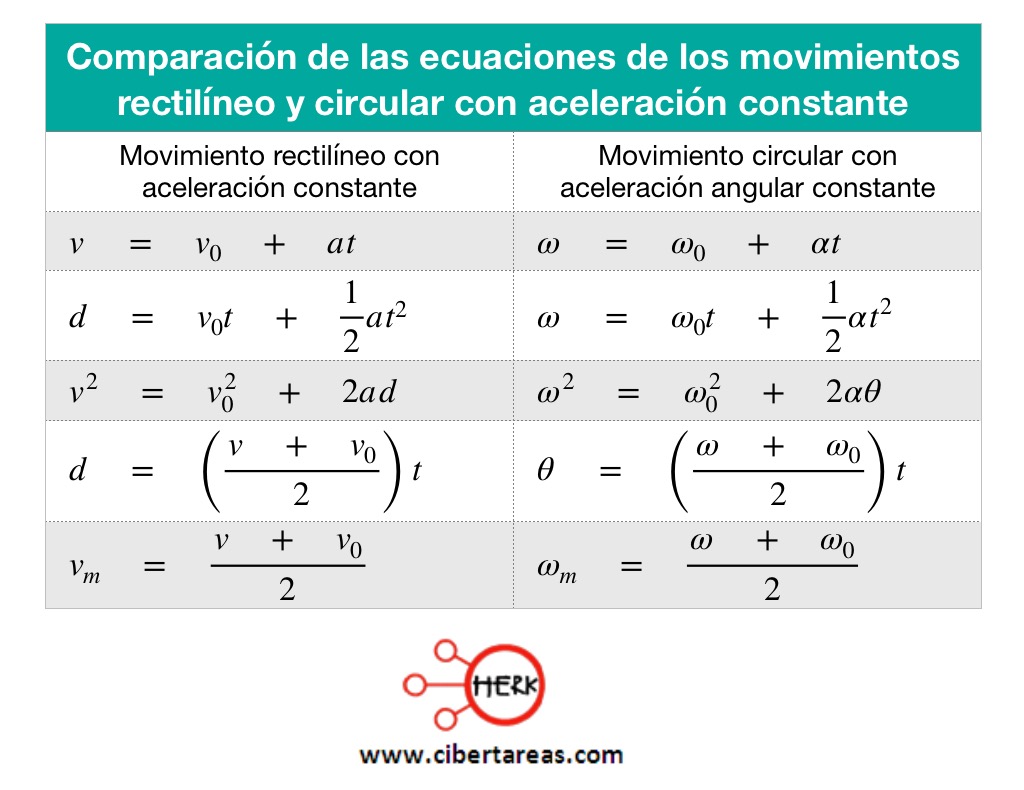
Al aplicar las ecuaciones del movimiento circular se deben elegir las unidades apropiadas para cada cantidad y conservar la convención para asignar a cada cantidad los signos apropiados según el sentido de rotación del cuerpo
Ejemplo:
Problema
-Una rueda gira con aceleración angular constante de 4 rad/s2
-Si la velocidad angular inicial tiene un valor de 2 rad/s en el instante t0 = 0 s
-¿Cuál es el valor del desplazamiento angular a los 20 s?
-¿Con qué rapidez angular gira a los 20 s?
Solución
-Valor de desplazamiento angular
-Datos
t0 = 0 s
𝜔0 = 2 rad/s
𝛼 = 4 rad/s2
t = 20 s
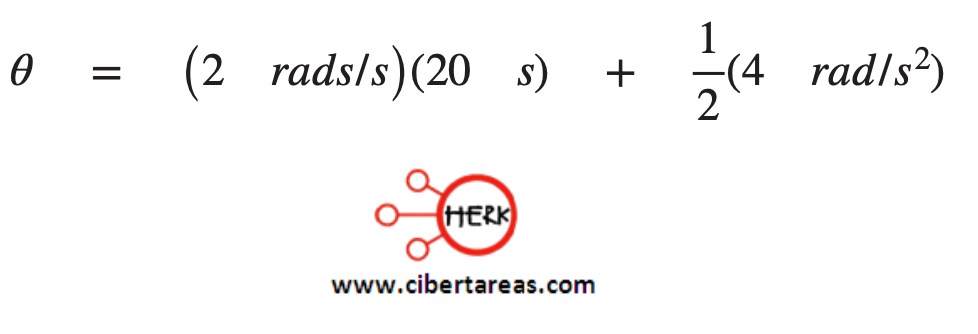
𝛳 = ? (20 s)2
Resultado
𝛳 = 840 rad
-Magnitud de la velocidad angular (rapidez angular) de la rueda
-Datos
t0 = 0s
𝜔0 = 2 rad/s
𝛼 = 4 rad/s2
t = 20 s
𝜔 = ?
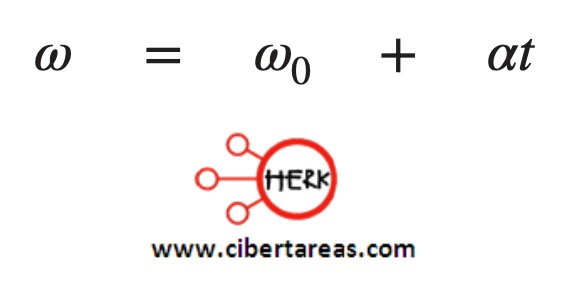
-Formula
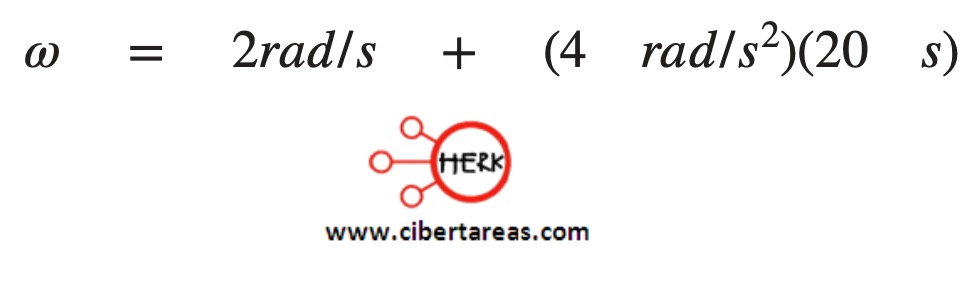
-Sustitución
-Resultado
𝜔 = 82 rad/s