Signos y valores de las funciones trigonométricas en Matemáticas 2

Para este tema es necesario determinar el ángulo agudo de referencia que conforma cada cuadrante, se debe deducir el signo que tienen las funciones trigonométricas en estos cuadrantes

Observemos los objetos inscritos en el plano cartesiano de la siguiente figura: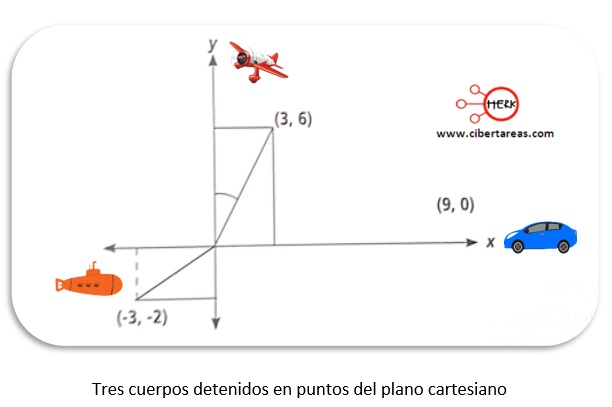

Con la figura anterior se puede observar un acercamiento bidimensional para aplicar los signos ( +, -) a los objetos según su ubicación

Cabe mencionar que la posición en el plano cartesiano está definida por sus respectivas coordenadas (x, y)

Al analizar la posición (x, y) el avión en el primer cuadrante de la figura anterior tenemos que se puede deducir el signo de las funciones trigonométricas que se forman con respecto al ángulo de referencia β

La distancia puede entenderse como una función que asigna un valor dependiendo de la posición del objeto y el punto de referencia

Ejemplo

-Se utiliza el teorema de Pitágoras para determinar la distancia del origen al submarino de la siguiente figura: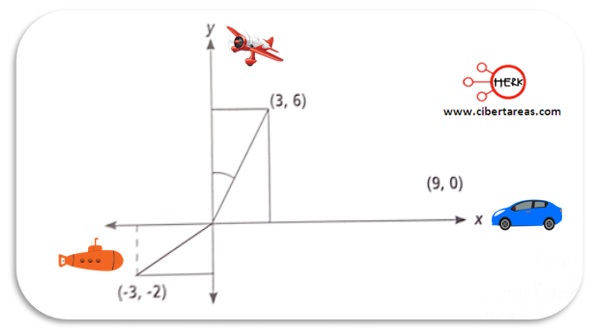

-Ya que por construcción se conforma un triángulo rectángulo

Solución

-Datos

-Las longitudes de los catetos son:

x: de 0 a -3, d = 3

y: de 0 a -2, d = 2

-Análisis

-La distancia d del origen (0, 0) a (-3, -2) es, por el teorema de Pitágoras:

d² = (3)² + (2)²

d² = 9 + 4

d = 

-Síntesis interpretativa

-Si directamente se escriben los valores negativos en la expresión pitagórica, se observa que:

d² = (-3)² + (-2)²

d² = 9 + 4

d = 

-Se pude concluir que la misma estructura de la relación pitagórica que permite calcular distancias desprende siempre valores positivos para cualquiera de los números, una de las características es que la distancia siempre es positiva

Tenemos que las posiciones del avión y del submarino permiten reconocer en la tabla siguiente los valores para las funciones básicas:

-Seno

-Coseno

-Tangente

Esto en los cuadrantes II, III, IV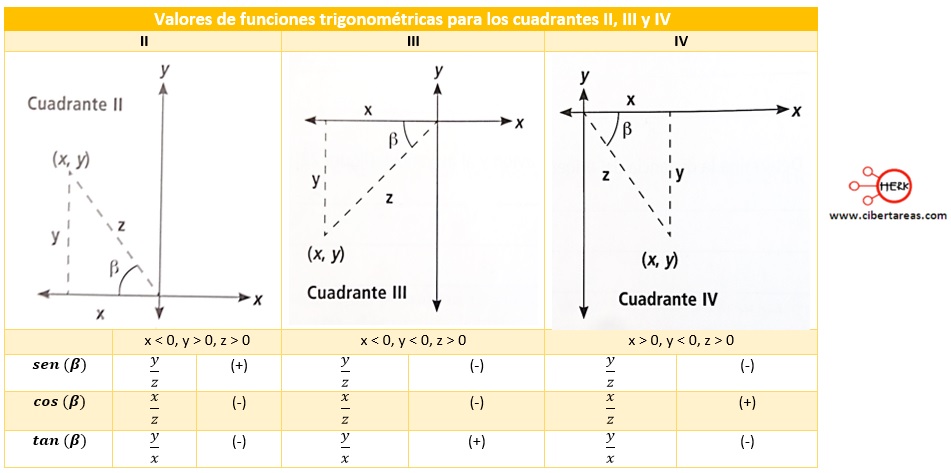

Los valores de las funciones trigonométricas para cada cuadrante están en la frase:

-Todos SENtimos TANtas COSitas

En el cuadrante I:

-Todos los valores son positivos

En el cuadrante II:

-Solo el seno y su reciproco son positivos

En el cuadrante II

-Solo la tangente y su reciproco son positivos

En el cuadrante IV

-Solo el coseno y su reciproco son positivos