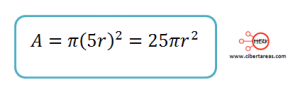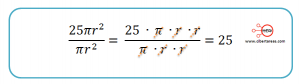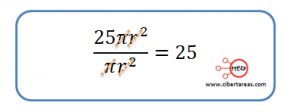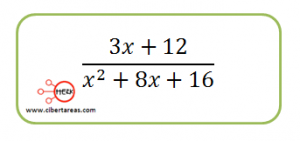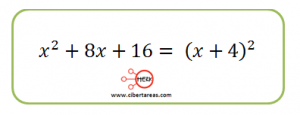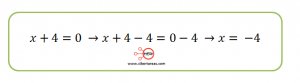Simplificacion de fracciones algebraicas
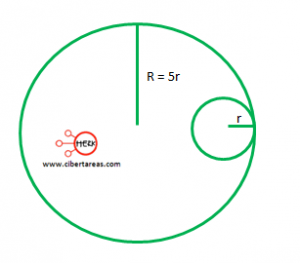
Supongamos que tenemos dos círculos que asemejan dos tapas de frascos de jugo, en la imagen se muestra la proporción de cada una de ellas
¿Cuántas circunferencias del círculo pequeño caben en el grande?
Analizando la imagen tenemos que la radio de la tapa menor cabe cinco veces en el radio de la tapa mayor, tenemos que:
Área del círculo
Como tenemos el valor del radio, sustituimos dicho valor
El área del círculo pequeño es:
Teniendo el tamaño de los dos círculos establecemos el cociente:
Podemos insertar 25 circunferencias de la tapa pequeña en la tapa grande
También podemos obtener el resultado directamente
Mapa conceptual de Simplificacion de fracciones algebraicas
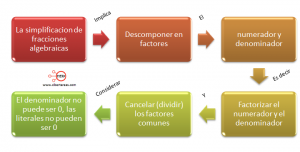
Con el concepto anterior vamos a deducir un mecanismo para simplificar una expresión de este tipo
Ejemplo
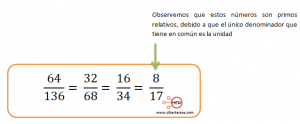
• Se divide el numerador y denominador por el numero primo 2
• No fue posible obtener la mitad exacta de 17 en la última fracción, por eso se detuvo el proceso de simplificación
Ejemplo
Teniendo la siguiente fracción algebraica, simplificarla
Al analizar las características de los elementos de la fracción algebraica, tenemos que el numerador tiene múltiplos de 3, y se factoriza de la siguiente manera:
El denominador es un trinomio cuadrado perfecto, entonces tenemos que:
De esta manera podemos sustituir en la fracción y cancelar
El resultado del ejemplo, solo tiene sentido si consideramos qué valores del denominador no pueden tomar la expresión (x + 4)
Se procede a igualar la ecuación a 0
Por lo tanto el resultado de nuestro ejemplo tiene una restricción (x ≠ -4), para cualquier otro valor de x no habría problema