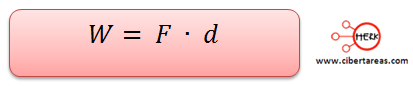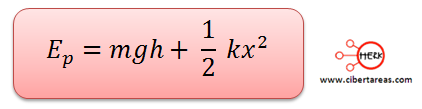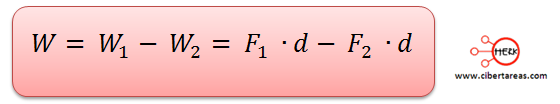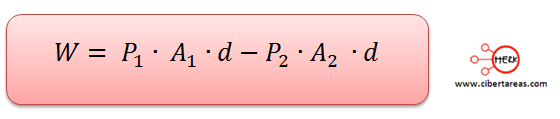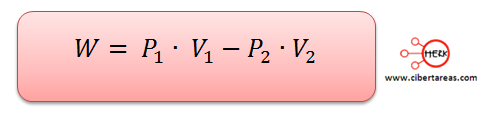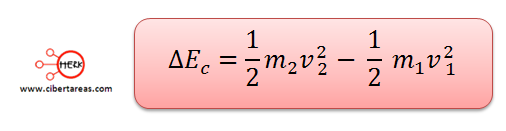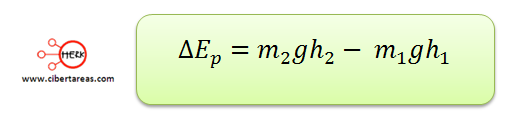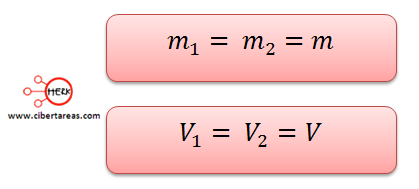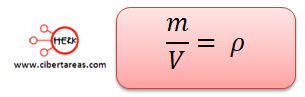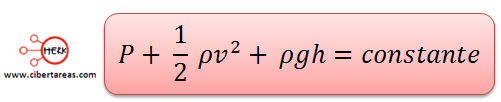Teorema de Bernoulli
Daniel Bernoulli, retomo uno de los principios en el análisis de la respuesta de los sólidos a las fuerzas que actúan sobre ellos (trabajo y energía) y lo aplico en la mecánica de fluidos, los resultados de los experimentos lo llevaron a concluir que:

Ejemplo del flujo de un líquido en una manguera.
Desarrollando el teorema, aplicamos el principio de trabajo (W) y energía (E), este principio nos señala que el trabajo realizado por todas las fuerzas efectivas es igual al cambio en la energía mecánica total del sistema, es decir:
Tenemos que las definiciones generales señalan que el trabajo se calcula mediante:
La energía cinética es:
Y tenemos que la energía potencial es:
Al aplicar tales definiciones al análisis de movimiento del fluido, el trabajo realizado esta dado por la suma del trabajo de todas las fuerzas activas
Como la fuerza que actúa en cada sección depende directamente de la presión que se ejerce en el área transversal, observamos que:
Sustituyamos en la siguiente educación:
Como resultado tenemos:
Como el volumen es A · d, entonces obtenemos finalmente que:
Tenemos que la energía cinética neta es:
Por otro lado tenemos que la energía potencias corresponde solo con l energía producida por la acción del campo gravitacional, que se asume que las propiedades elásticas del agua con nulas por lo que no existe la energía potencial elástica
Sustituimos las siguientes ecuaciones
En ésta, la ecuación general
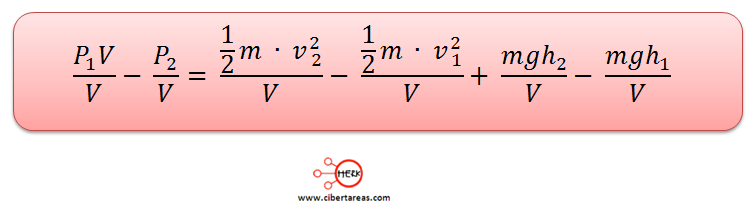
Tenemos como resultado:
Consideramos que el volumen del fluido es el mismo en cada sección, tenemos que:
Y al sustituir la masa y dividir entre el volumen, tenemos que:
Para finalizar y recordamos que
Y ordenamos la expresión anterior podemos concluir que:
O podemos tener:
Las 2 ecuaciones anteriores son las dos formas que toma el modelo matemático del principio de Bernoulli y estas nos indican que:
La presión se mantiene invariable entre dos puntos cualesquiera de una tubería por la geometría de la misma (refiriéndose a los cambios de altura) y por el comportamiento del flujo (estos son los cambios de velocidad, asumiendo que la viscosidad es nula (por esta razón no existe perdida de energía)
Estas ecuaciones son validad en un gran número de situaciones prácticas, debido a que el error es mínimo.