El punto de Inflexión en Máximos y Mínimos en Cálculo Diferencial, una función f presenta un punto de inflexión en [c, f(c)] si es continua en ese punto y además separa dos arcos de concavidad opuesta.
Mes: julio 2018
Los Relativos con el criterio de la primera derivada en máximos y mínimos – Cálculo Diferencial
Los Relativos con el criterio de la primera derivada en máximos y mínimos – Cálculo Diferencial
Como criterio de la primera derivada para calcular los máximos y míimos relativos de una función.
1.- Calcular la derivada de y=f(x)
2.-Al igualar a cero la derivada de y=f(x) y resolver la ecuación, estas soluciones se omitir algunos valores críticos.
3.-Analizar el siglo de dy/dx un valor antes y uno después de cada valor crítico sin omitir alguno de ellos.
Las Funciones Crecientes y Decrecientes variables en producciones, máximos y mínimos – Cálculo Diferencial
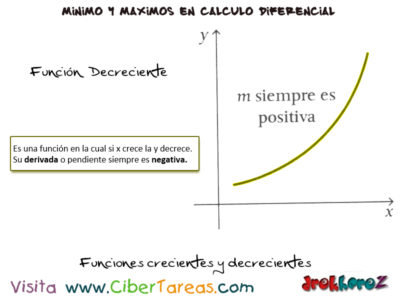
Las Funciones Crecientes y Decrecientes variables en producciones, máximos y mínimos en cálculo diferencial analizar si las funciones son crecientes o decrecientes y observemos es la pendiente o derivada en cada punto de las gráficas.
1.- Función Decreciente: Es una función en la cual si x crece la y decrece. u derivada o pendiente siempre es negativa.
Los Ejemplos de las producciones, máximos y mínimos relativos – Calculo Diferencial
Los Ejemplos de las producciones, máximos y mínimos relativos en Calculo Diferencial, en la función y=2-x2 tiene un solo valor máximo absoluto y local en x=0 dado que f(0)=2 es el valor más grande que adquiere el rango.
Como podemos observar en la gráfica de la parábola de la derecha, no existe el punto mínimo.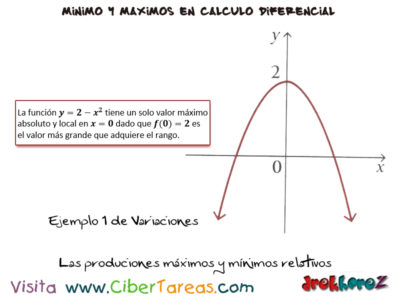
Variaciones en las producciones máximos y mínimos relativos – Cálculo Diferencial
Variaciones en las producciones máximos y mínimos relativos en Calculo Diferencial, donde la derivada siempre es horizontal por lo tanto es igual a cero.
Existen métodos más exhaustivos que nos garantizan encontrar dichos [Máximos y Mínimos] de una función a partir de funciones con valores extremos donde la derivada no es cero o bien donde la derivada en un punto de una gráfica sea igual a cero y la función no sea un valor máximo o un valor mínimo.
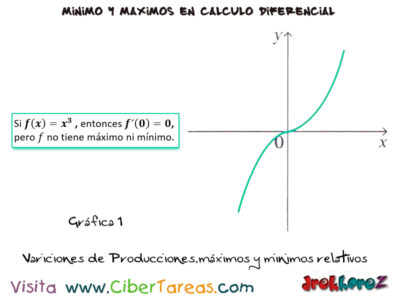
1.- Si f(x)=x3 entonces f'(0)=0 pero f no tiene máximo ni mínimo.