Limite de Funciones Polinomiales en Cálculo Diferencial basta con utilizar a siguiente regla básica de limites:
Categoría: Calculo Diferencial
Limite de una Función en una tabla, gráfica y aplicación – Cálculo Diferencial
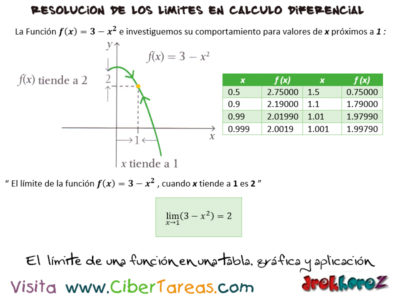
El Límite de una Función en una tabla, gráfica y aplicación en el Cálculo Diferencial, ahora lo estudiaremos con más precisión y extensión el concepto de limite y los métodos para calcularlo.
Utilizaremos el ejemplo de la función:
f(x) = 3 – x2
Su comportamiento para los valores de [x] próximos a 1.
Velocidad instantánea en una tabla, gráfica y aplicación – Cálculo Diferencial
Velocidad Instantánea en una Tabla,gráfica y aplicación en el Cálculo Diferencial, la mismo idea de limite surge en las situaciones donde queremos calcular la velocidad de un objeto en un instante dado.
La distancia s[t] en metros recorrida por un objeto que se deja caer después de [t] segundos se puede encontrar con la expresión s(t)= 3.7t2. Para determinar la velocidad después de 6 segundos.
Tangente de una curva en los limites en una tabla, gráfica y aplicación – Cálculo Diferencial
Tangente de una curva en los limites en una tabla, gráfica y aplicación en Cálculo Diferencial para conocer cómo surgen los “Límites” a partir de la tangente a una curva.
-Necesitamos tener un punto y la pendiente de una recta para determinar su ecuación.
-Calcular la pendiente “m” de una recta es necesario conocer dos de sus puntos.
-Ya que solo con conocer el punto fijo P[1,1], entonces aproximamos la pendiente de “m” de la recta tangente eligiendo un punto móvil Q [x,x2] de la función cercana a “P” y calculamos la pendiente [mPQ] con la expresión
Límite de una serie en los Modelos Matemáticos – El estudio del Cálculo y su evolución – Cálculo Diferencial
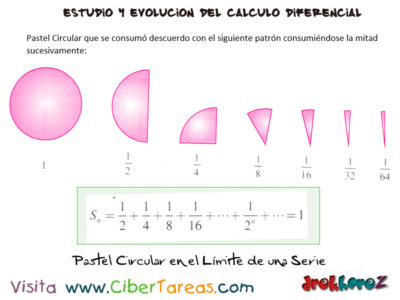
Limite de una Serie en los Modelos Matemáticos en el estudio del Cálculo y su evolución del calculo Diferencial, utilizaremos como ejemplo un Pastel Circular que se consume desacuerdo con el siguiente patrón:
El primer día se come la mitad, al día siguiente la otra mita que queda, al tercer día de nuevo se consume la mitad que queda y así sucesivamente observa la siguiente imagen: