Ejemplos de calculo de máximos y mínimos relativos con el criterio de la primera derivada en el Calculo Diferencial en la función y=x3 – 6x2 + 9x y después elaborar la gráfica correspondiente.
Al calcular la derivada e la función:
dy/dx=3x2 -12x + 9
Etiqueta: calculo diferencial
El punto de Inflexión en Máximos y Mínimos – Cálculo Diferencial
Los Relativos con el criterio de la primera derivada en máximos y mínimos – Cálculo Diferencial
Los Relativos con el criterio de la primera derivada en máximos y mínimos – Cálculo Diferencial
Como criterio de la primera derivada para calcular los máximos y míimos relativos de una función.
1.- Calcular la derivada de y=f(x)
2.-Al igualar a cero la derivada de y=f(x) y resolver la ecuación, estas soluciones se omitir algunos valores críticos.
3.-Analizar el siglo de dy/dx un valor antes y uno después de cada valor crítico sin omitir alguno de ellos.
Variaciones en las producciones máximos y mínimos relativos – Cálculo Diferencial
Variaciones en las producciones máximos y mínimos relativos en Calculo Diferencial, donde la derivada siempre es horizontal por lo tanto es igual a cero.
Existen métodos más exhaustivos que nos garantizan encontrar dichos [Máximos y Mínimos] de una función a partir de funciones con valores extremos donde la derivada no es cero o bien donde la derivada en un punto de una gráfica sea igual a cero y la función no sea un valor máximo o un valor mínimo.
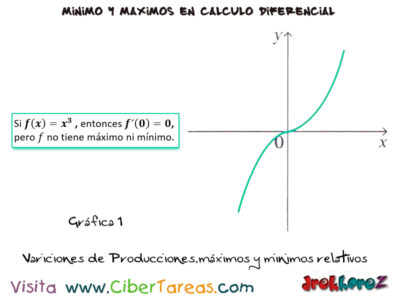
1.- Si f(x)=x3 entonces f'(0)=0 pero f no tiene máximo ni mínimo.
Ejemplos de la Producción, Máximos y Mínimos – Cálculo Diferencial
Ejemplos de la Producción, Máximos y Mínimos en Cálculo Diferencial,primer problema como ejemplo:
1.-Un terreno que mide 100 metros de perímetro y desea expresar su área A como función de la base x para calcula la medida de la base y de la altura que nos da la figura de mayor superficie.
Vamos a escoger tres posible rectángulos cuyo perímetro es de 100 metros para tener idea que ocurre en el problema, las dimensiones que se obtiene.
Al conocer las medidas del rectángulo vemos las variables en cuestión:
